Оглавление:



Гиперболические функции
- Гиперболическая функция. Функция- — — — — — — — и———-соответственно Р и П Е Р Б О Л И Ч Е С К и М О Н м и Г и П Е Р Б О Л И Ч Е С К и М и Н м называют символ » Х » и подобные.: айхе zich= Гиперболический
тангенс и гиперболическая смежность соответственно определяются выражением ,и Z Х-ех-Е~Х,,, Х Х Х EX4 В-Е~Х Ш х= = ———-, Ш. х= = -1 — ХН ХН+ХН ХН-е Из определения гиперболических
функций: гиперболический Косинус, гиперболический синус и Людмила Фирмаль
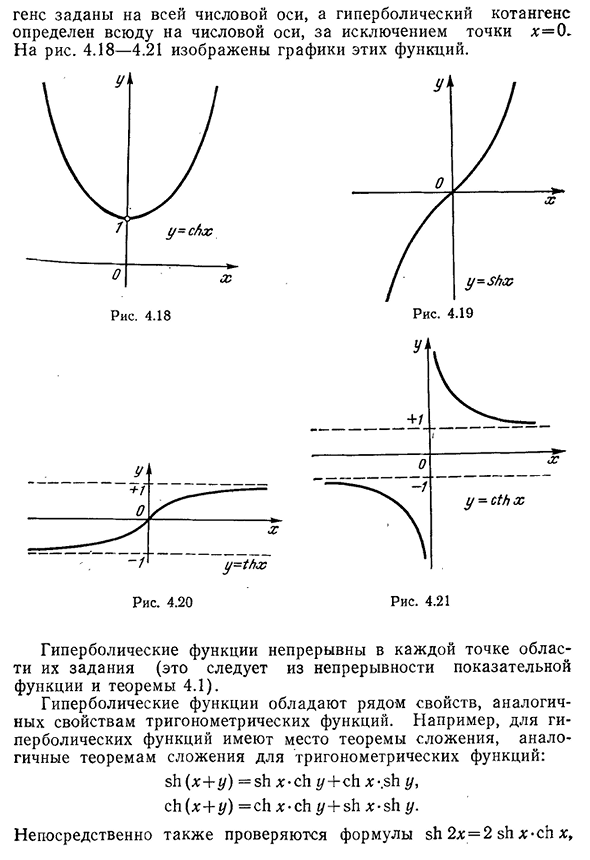
гиперболическое пожелтение — §3. Начальная школа функция начальной школы 157 Ген задается по всей числовой оси, и гиперболическая собираемость определяется везде на числовой оси,
за исключением точки x=0. Для риса. 4.18-4.21 отображаются графики этих функций. Гиперболические функции непрерывны во всех точках области их назначения (это следует из непрерывности экспонент и
- теоремы 4.1). Гиперболические функции обладают многими свойствами, сходными с тригонометрическими функциями. Например, для гиперболических функций существует теорема
сложения, аналогичная теореме сложения тригонометрических функций: zy (x+y)=zy x-XY g/+XY x -.З. Ы. У Сы(х+»/)=Си х-Сы г/+З. ы. х-з. ы. у. Формула zy2x=2zy x-XY x, 158Chapter4 также непосредственно проверяется. Непрерывность функций ey2x-ey2x-1.
Эпитет «гипербола» связан с тем, что знак равенства x=a-C111, y=a-zY задает гиперболу как Людмила Фирмаль
знак равенства x=A-SO8/, g/=C-8sh/. В самом деле, в первом случае раскрывается уравнение x2—Y2=A2, то есть гиперболическое, а во втором-уравнение окружности x2+Y2=A2.
Смотрите также:
Методическое пособие по математическому анализу
| Производные тригонометрических функций | Признаки монотонности функции |
| Обратные тригонометрические функции | Краткие сведения о комплексных числах |

