Оглавление:
Гипербола
Каноническое уравнение гиперболы
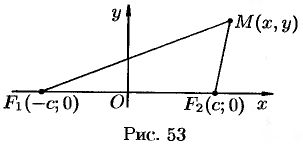
Гиперболой называется множество всех точек плоскости, модуль разности расстояний от каждой из которых до двух данных точек этой плоскости, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.
Обозначим фокусы через 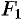 и
и 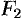 , расстояние между ними через
, расстояние между ними через 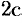 , а модуль разности расстояний от каждой точки гиперболы до фокусе через
, а модуль разности расстояний от каждой точки гиперболы до фокусе через 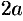 . По определению
. По определению 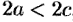 , т.е.
, т.е. 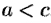 .
.
Для вывода уравнения гиперболы выберем систему координат 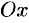 так, чтобы фокусы
так, чтобы фокусы 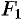 и
и 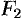 лежали на оси
лежали на оси 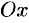 , а начало координат совпало с серединой отрезка
, а начало координат совпало с серединой отрезка 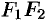 (см. рис. 53). Тогда фокусы будут иметь координаты
(см. рис. 53). Тогда фокусы будут иметь координаты 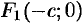 и
и 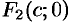 .
.
Пусть 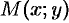 — произвольная точка гиперболы. Тогда согласно определению гиперболы
— произвольная точка гиперболы. Тогда согласно определению гиперболы 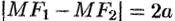 или
или 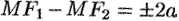 , т. е.
, т. е. 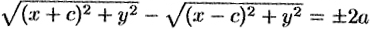 . После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы
. После упрощений, как это было сделано при выводе уравнения эллипса, получим каноническое уравнение гиперболы

где

Гипербола есть линия второго порядка.
Исследование формы гиперболы по ее уравнению
Установим форму гиперболы, пользуясь ее каноническим уравнением.
1. Уравнение (11.9) содержит 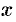 и
и 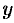 только в четных степенях. Следовательно, гипербола симметрична относительно осей
только в четных степенях. Следовательно, гипербола симметрична относительно осей 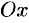 и
и 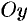 , а также относительно точки
, а также относительно точки 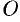 (0; 0), которую называют центром гиперболы.
(0; 0), которую называют центром гиперболы.
2. Найдем точки пересечения гиперболы с осями координат. Положив 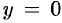 в уравнении (11.9), находим две точки пересечения гиперболы с осью
в уравнении (11.9), находим две точки пересечения гиперболы с осью 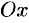 :
: 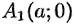 и
и 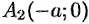 . Положив
. Положив 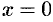 в (11.9), получаем
в (11.9), получаем 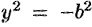 — чего быть не может. Следовательно, гипербола ось
— чего быть не может. Следовательно, гипербола ось 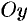 не пересекает.
не пересекает.
Точки 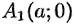 и
и 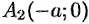 называются вершинами гиперболы, а отрезок
называются вершинами гиперболы, а отрезок 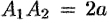 — действительной осью, отрезок
— действительной осью, отрезок 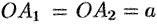 — действительной полуосью гиперболы.
— действительной полуосью гиперболы.
Отрезок 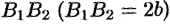 , соединяющий точки
, соединяющий точки 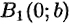 и
и 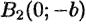 называется мнимой осью, число
называется мнимой осью, число 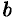 — мнимой полуосью. Прямоугольник со сторонами
— мнимой полуосью. Прямоугольник со сторонами 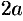 и
и 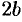 называется основным прямоугольником гиперболы.
называется основным прямоугольником гиперболы.
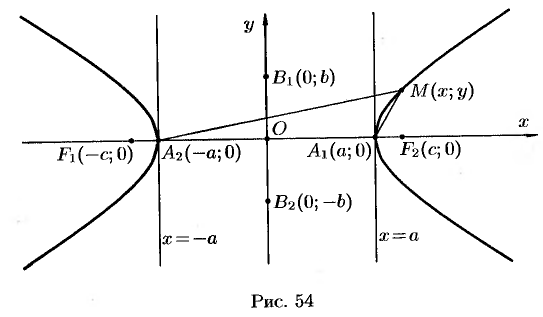
3. Из уравнения (11.9) следует, что уменьшаемое 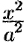 не меньше единицы, т. е. что
не меньше единицы, т. е. что 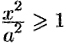 или
или 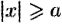 . Это означает, что точки гиперболы расположены справа от прямой
. Это означает, что точки гиперболы расположены справа от прямой 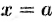 (правая ветвь гиперболы) и слева от прямой
(правая ветвь гиперболы) и слева от прямой 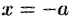 (левая ветвь гиперболы).
(левая ветвь гиперболы).
4. Из уравнения (11.9) гиперболы видно, что когда 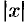 возрастает,
возрастает,
то и 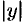 возрастает. Это следует из того, что разность
возрастает. Это следует из того, что разность 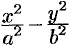 сохраняет постоянное значение, равное единице.
сохраняет постоянное значение, равное единице.
Из сказанного следует, что гипербола имеет форму, изображенную на рисунке 54 (кривая, состоящая из двух неограниченных ветвей).
Асимптоты гиперболы
Прямая 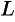 называемся асимптотой неограниченной кривой
называемся асимптотой неограниченной кривой 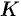 , если расстояние
, если расстояние 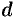 от точки
от точки 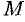 кривой
кривой 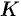 до этой прямой стремится к нулю при неограниченном удалении точки
до этой прямой стремится к нулю при неограниченном удалении точки 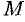 вдоль кривой
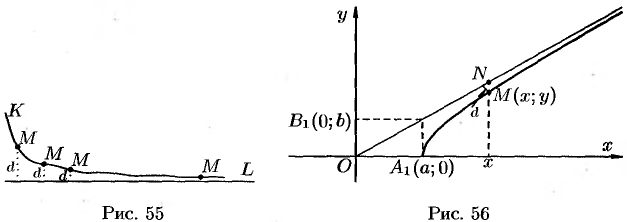
вдоль кривой 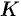 от начала координат. На рисунке 55 приведена иллюстрация понятия асимптоты: прямая
от начала координат. На рисунке 55 приведена иллюстрация понятия асимптоты: прямая 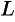 являемся асимптотой для кривой
являемся асимптотой для кривой 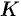 .
.
Покажем, что гипербола 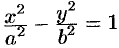 имеет две асимптоты:
имеет две асимптоты:
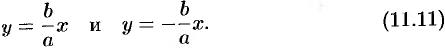
Так как прямые (11.11) и гипербола (11.9) симметричны относительно координатных осей, то достаточно рассмотреть только те точки указанных линий, которые расположены в первой четверти.
Возьмем на прямой 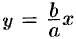 точку
точку 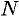 имеющей ту же абсциссу
имеющей ту же абсциссу 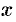 , что и точка
, что и точка 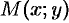 на гиперболе
на гиперболе 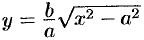 (см. рис. 56), и найдем разность
(см. рис. 56), и найдем разность 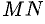 между ординатами прямой и ветви гиперболы:
между ординатами прямой и ветви гиперболы:
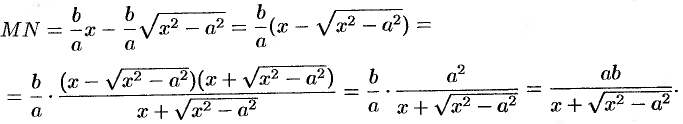
Как видно, по мере возрастания 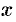 знаменатель дроби увеличивается; числитель -— есть постоянная величина. Стало быть, длина отрезка
знаменатель дроби увеличивается; числитель -— есть постоянная величина. Стало быть, длина отрезка 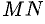 стремится к нулю. Так как
стремится к нулю. Так как 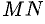 больше расстояния
больше расстояния 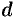 от точки
от точки 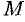 до прямой, то
до прямой, то 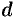 и подавно стремится к нулю. Итак, прямые
и подавно стремится к нулю. Итак, прямые 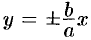 являются асимптотами гиперболы (11.9).
являются асимптотами гиперболы (11.9).
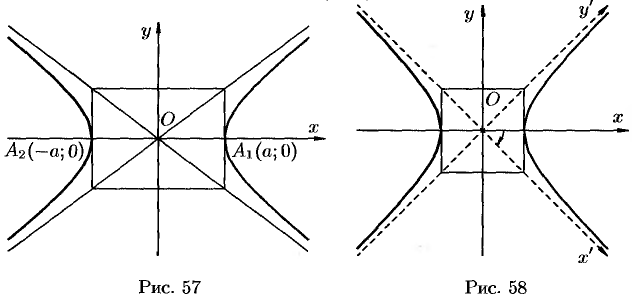
При построении гиперболы (11.9) целесообразно сначала построить основной прямоугольник гиперболы (см. рис. 57), провести прямые, проходящие через противоположные вершины этого прямоугольника, — асимптоты гиперболы и отметить вершины 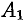 и
и 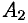 гиперболы.
гиперболы.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Окружность |
| Эллипс |
| Парабола |
| Общее уравнение линий второго порядка |

