Гидравлический прыжок в руслах переменного по длине сечения (в непризматических руслах).

Оглавление:

Это изображение имеет пустой атрибут alt; его имя файла - image-10-1.png

Гидравлический прыжок в руслах переменного по длине сечения (в непризматических руслах).

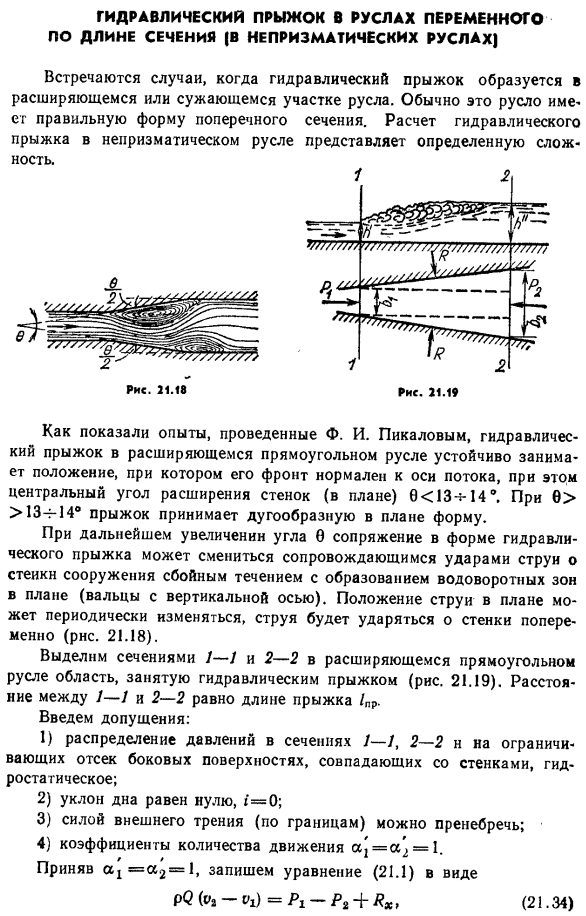
Гидравлический прыжок в руслах переменного по длине сечения (в непризматических руслах]. Гидравлические скачки могут образовываться на увеличенных или уменьшенных участках водотока. Как правило, этот канал имеет правильную форму поперечного сечения. Расчет гидравлического прыжка на призму канала сопровождается определенной сложности. Рисунок 21.19 Ф. И… Как показал проведенный Пикаловым эксперимент, гидравлический скачок в расширяющемся прямоугольном канале занимает устойчивое положение, фронт которого перпендикулярен оси потока, а центральный угол расширения стенки(в плане) равен 0С13+ 140. Если 0 > > 13 −14°, скачок имеет дугообразную форму. При еще большем угле 0 конъюгат в виде гидравлического скачка может быть заменен струйным потоком со струйным ударом в здании с неисправным потоком (роликом с вертикальной осью) с образованием спиральной зоны в плане.

Встречаются случаи, когда гидравлический прыжок образуется в расширяющемся или сужающемся участке русла. Обычно это русло имеет правильную форму поперечного сечения. Людмила Фирмаль

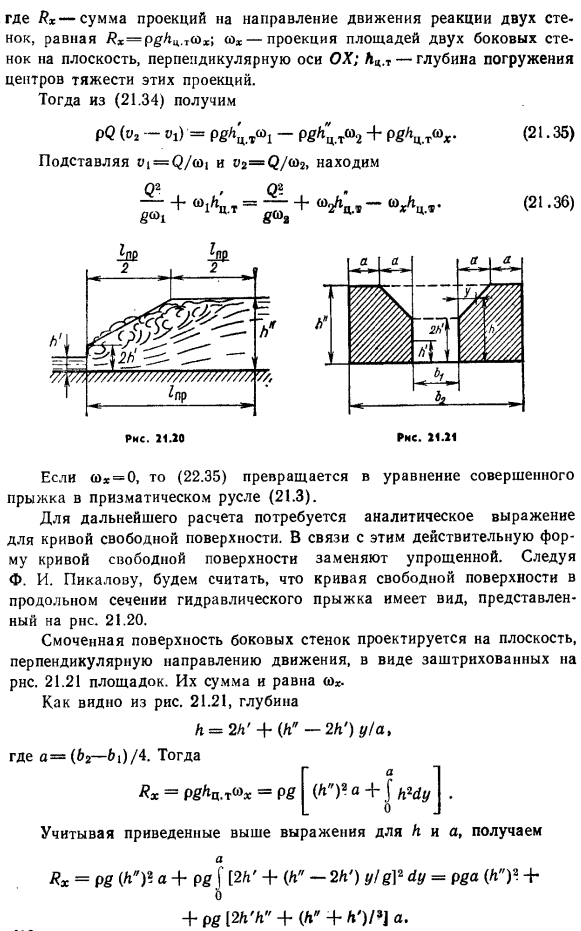
Расположение струи в плане можно периодически менять, и струя будет поочередно ударяться о стену (номер 21.18). Выделите участки 1-1 и 2-2 расширяющегося прямоугольного канала в качестве площади, занимаемой гидравлическим скачком (рис. 21.19). Расстояние между 1-1 и 2-2 равно длине прыжка 1pr. Мы введем предпосылку. 1) сечение от 1 до 1 сторон, образующих границу отсека, совпадающую со стенкой, распределение давления 2-2 Н является гидростатическим. 2) градиент внизу равен нулю,» ’ = 0; 3) сила внешнего трения (вдоль границы) пренебрежимо мала. 4) коэффициент импульса ss / = a » 2 = 1. /// взяв a1 = a2 = 1, Запишите формулу(21.1)в следующем виде: (21.34） Р 2(ОА-о)= ПМ-Р2 + 411. Где хх-сумма проекций в направлении реакции двух стенок, равная ХΧ = § ЛЦ. cx-проекция площади 2 боковых стенок в плоскость, перпендикулярную оси OX. Легкие танки. t-глубина погружения центроида этих проекций.

Затем получить его из(21.34) p 2 (y2-Tm)=ё!/!Т. tsh1-П ^ Т. ТМ2 + П ^Т. Т<sup class=»reg»>®</sup>*-(21.35） Когда вы назначаете = и V2 = ^ / n、 5:+=; & + » L.-L.(21-36)） Для (Ox-0), (22.35) будет уравнение для полного скачка призмы канала(21.3). Дальнейшие расчеты требуют аналитической формулы для кривой свободного surface. In в связи с этим фактическая форма кривой свободной поверхности заменяется упрощенной. Ф. И… Вслед за Пикалевым предположим, что кривая свободной поверхности продольного сечения гидравлического скачка имеет вид, указанный в РНС. 21.20. Смоченная поверхность боковин проецируется на плоскость, перпендикулярную направлению движения, штрихованную к РНС. 21.21 сайт. Их сумма будет равна wx. Как видно из рисунка 21.21, глубина Где а =(62-160 / 4. Я * = Pvcc. т ^ х = П8 А = 2А ’ +(а «-2а’) г / с、 Учитывая приведенное выше уравнение для I и a、 Но… = х = П8(* ’)* »+ второй [2А’ + {к» 2А’) г!§ ] * Лу = p8a(к «)2. + о 412. + П8 [2К Купянск „а +(„■+к ’） Как известно, для прямоугольного канала、 СО1-d1L>; а ^ м = 0,5 а; ©2 = л ^ м = 0,5 л. Понял?Χ, 1 1, rr, ц, подставляя значение ц _ в (21.35), при приведении к ρ、 („2 _ 01)= Y1 ( * ’) 1/2 (A“) “/ 2 +(Л’)?А+ 8. + [2А ’ а „+(а“ 2-е’) / 3] а. V \ = SC (L \ kg) и P2 =? Подставляя (*2L“) и выполняя преобразование, получаем уравнение гидравлического скачка непризматического укрупненного канала прямоугольного сечения. 6(?2 602. + ( »» )?(*,+ 2y2) К «К ’(В2-В2)= Р-7 +(’ ’)?(* 1 + 2y2).8<sup class=»reg»>®</sup>rA 8 * 1» (21.37） Ширины каналов секций 1-1 и 2-2 соединяются следующим образом: * a = * 1 + 2 / Пр18б. Здесь задается угол 0, а длина гидравлического скачка определяется по одной из известных формул.1. в глубине и сопряженный.

Как показали опыты, проведенные Ф.И. Пикаловым, гидравлический прыжок в расширяющемся прямоугольном русле устойчиво занимает положение, при котором его фронт нормален к оси потока. Людмила Фирмаль

Тогда, поскольку известна 1 из сопряженных глубин, ширина обоих участков известна после вычисления 1 из них, поэтому поток (2) известен, а в Формуле (21.37) неизвестными остаются только другие сопряжения. Если & 1 = * 3, то формула (21.37) будет полной формулой гидравлического скачка в канале прямоугольного сечения. отметим, что помимо линейной аппроксимации k используется также представление глубины поперечного сечения в виде параболы. K и K ’+(К»-К’) (К / А) Т、 Где показатель-среднее значение t-0,25. Гидравлический скачок в радиальном растекающемся потоке в прямоугольном сечении колонного канала. Окей. F. мы даем решение, полученное путем Vasiliev. In горизонтальный день, идеальный гид На первом участке (глубина k’), когда радиальное распространение потока в шероховатом состоянии обеспечено, можно равномерно прыгать при 6 > 13-d-14°, не отходя от стенки. Такие условия могут быть созданы из-под кривой в точке затвора или при ее истечении из кривой (в плане). 413. Отверстие. Обе структуры должны быть очерчены по радиусу(в плане) (рис. 21.22). Гидравлический прыжок ограничен участками 1-1 (глубина k’) и 2-2 (глубина k«), изогнутыми в плоскости. Использование Полярных Координат、 о «^ = к’yyy; о) = к » Р20、 Где 9 = i / 180; 0О= 0° / 57.3-расширенный угол в радианах. rx и r2 соединены по глубине с радиусом окружности секций k ’и k’, а r и r2 соединены между собой. Р2= р+/ и т. д. Удельные расходы потока секций 1-1 и 2-2 равны 41 = 41 ^ 1?); 7а = = = 0 / га. В первом разделе, это важно

Смотрите также:

Решение задач по гидравлике

Возможно эти страницы вам будут полезны: