Оглавление:






Гибкие нити
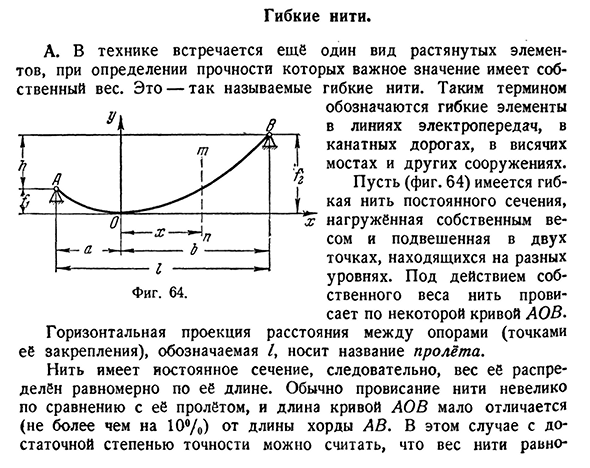
- Гибкая нить. A. In технология, есть еще один вид растяжения элемента, в определении прочности которого важна соб-гибкая нить. Этот термин относится к гибким элементам линий электропередач, канатных дорог, подвесных мостов и других сооружений. Пусть (рис. 64) имеется гибкая нить определенного сечения, нагруженная собственным весом и подвешенная в двух точках на разных уровнях. Под действием собственного веса нить свисает вниз по определенной кривой АОВ. Горизонтальная проекция расстояния между опорой (ее неподвижной точкой) обозначается Z и называется span.
Поскольку нить имеет определенное поперечное сечение, ее вес равномерно распределяется по всей длине. Провисание нити обычно меньше ее пролета, а длина кривой AOV мало отличается(менее 10%) от длины кода AB. В этом случае с достаточной точностью можно предположить, что вес нити равен§ 31] гибкой нити 109 Она распределена по размерам не по своей длине, а по длине проекции на горизонтальную ось. Эта нагрузка с длиной может быть не только мертвым грузом нити на единицу длины пролета, но и весом льда или других равномерно распределенных нагрузок. Предположения о законе распределения нагрузки являются important.
It позволяет легко вычислить, но в то же время приближенно; если в точном Людмила Фирмаль
решении (нагрузка распределена вдоль кривой) кривая lop является цепной линией, то в приближенном решении кривая lop является квадратным параболоидом. Начало координат выбирается в самой нижней точке свисающей нити О. 64), которая, будучи нам неизвестной, обнаруживает, что зависит от величины нагрузки qt, отношения длины струны в Кривой к длине пролета и относительного положения опорной точки. В точке О касательная к свободной кривой нити явно поперечна. Эта касательная направляет ось X-вправо. Вырезать две секции-от начала координат x
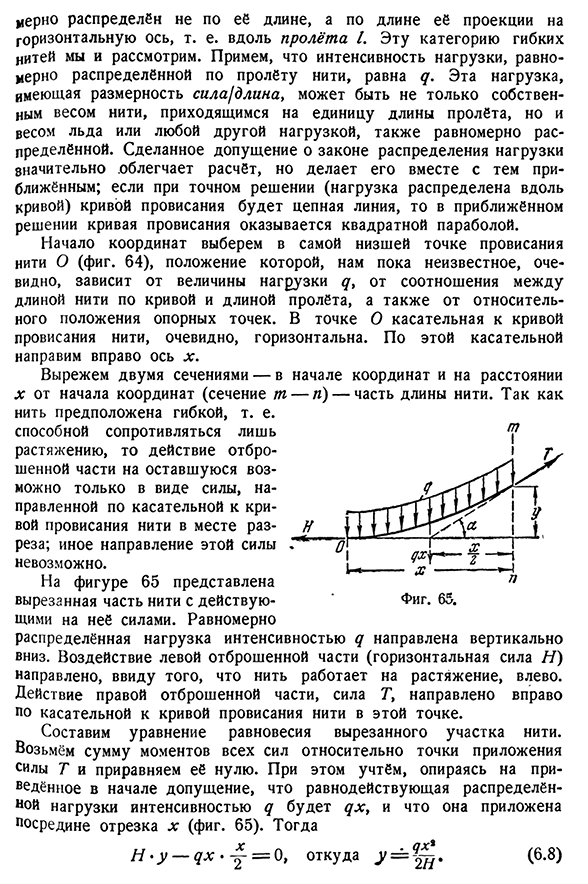
(секция n\нить является гибкой, т. е. может сопротивляться только растяжению, только с разрезом). На рисунке 65 показан отрезанный участок нити с силой, действующей на нить. Равномерно Начало и расстояние-n) — часть длины нити. С тех пор Фигура. Шестьдесят пять Распределение силы нагрузки Q направлено вниз в вертикальном направлении. Воздействие левой отбрасываемой детали (горизонтальная сила H)направлено влево, за счет того, что нить действует на натяжение. Сила G, являющаяся действием правой
- отбрасываемой детали, направлена вправо в контакте с провисающей кривой изгиба нити в этой точке. Составим уравнение равновесия отрезанной части нити. Возьмем сумму моментов всех сил относительно точки приложения силы T и будем считать ее равной нулю. В этом случае, исходя из предположения, приведенного вначале, считают, что результатом распределения силы нагрузки q является qx, которая приложена к середине отрезка x(рис. 65). Затем ГГ Н * м-м х * х=л * й=. За счет собственного веса при расширении и сжатии Oh(6.8) [гл. ВИ Свободный изгиб саней-это парабола. Если обе точки подвеса нити находятся на одном уровне, f x=/ — f. это легко определить из уравнения (6.8); в этом случае из-за симметрии нижняя точка нити находится в середине пролета,
то значение уравнения (6.8) A=B=B= -^: (6.9) Из этой формулы определите величину силы H: (6.10)) Величина H называется горизонтальным натяжением нити. Итак, если известны нагрузка q и напряжение H9, то по формуле (6.9) находим поникшую стрелку/. Учитывая Q и f, напряжение H определяется по формуле (6.10). Связь между этими значениями и длиной 5 нитей вдоль кривой провеса устанавливается с помощью приближенной формулы, известной из математики 1) (6.11) Вернемся к соображениям фиг. 65, то есть сумма проекций всех сил на ось Х к нулю: — Н~[~Т коса=0. Из этого уравнения мы находим силу t-натяжения в любой точке Из Формулы (6.12)видно, что сила t от самой нижней точки резьбы к опоре возрастает и становится максимальной в условиях подвеса.
При небольшом провисании нити этот угол не достигнет Мы приходим Людмила Фирмаль
к формуле (6.11). 32/А х\н — — — — — -). После интегрирования в диапазоне от c=0 до JC=Z/2 и удвоения§ 31] гибкая нить 111 Таким образом, с достаточной точностью на практике можно предположить, что сила в резьбе постоянна и равна ее натяжению N. Если необходимо рассчитать максимальную силу в точке подвеса, то для симметричной резьбы ее значение определяется следующим образом: вертикальные составляющие реакции опор равны между собой и равны половине суммарной нагрузки на резьбу, то есть горизонтальная составляющая равна силе L/, определяемой по формуле (6.10). Идеальная реакция носителя получается как геометрическая сумма этих составляющих: Условие прочности гибкого винта следующим образом когда площадь поперечного сечения показана F: Если заменить натяжение H на его величину
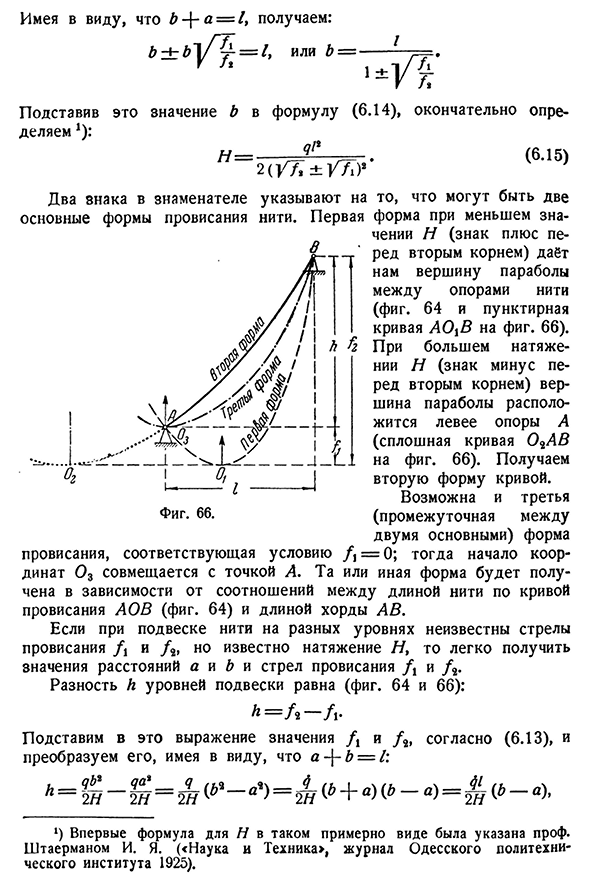
по формуле (6.10)、: Из этой формулы можно указать Z, q, F и[a], чтобы определить требуемое отклонение стрелы/. Если Q содержит только собственный вес, то решение упрощается, где q — ^^F9, где 7-вес единицы объема материала нити、 A8F 7 _7^ ’ [а|-8[а]’ То есть значение f не включается в расчет. B. Если точки подвеса нити находятся на разных уровнях, то при присвоении выражению (6.8) значений x—a и x=B>вы найдете/i и/2: /. = * * £. (Б-13) Поэтому из второго выражения мы определяем напряжение (6.14 )) И если мы разделим первое на второе, то 112 занимает самостоятельный вес напряжения и сжатия[гл. ВИ Имея в виду, что B — | — a=A получается: Назначить деление j): это значение b в выражении (6.14), и, наконец, opre- (6 1 5 ) Основная форма провисания пряжи. Первый В Фигура. Шестьдесят шесть Два знака в знаменателе указывают на то, что могут быть две формы с меньшим значением H(знак плюс перед
вторым корнем), показывающие нам пунктирную кривую AO^B на рисунке 64, которая поддерживает потоки. 66). При большем напряжении H(знак минус перед вторым корнем) вершина параболы расположена слева от опоры A (сплошная кривая O^AB на фиг. 66). Мы получаем вторую форму кривой. Третья (две основные промежуточные) форма провисания способна соответствовать условию/1=0; тогда начало координат O3 совмещается с точкой A. та или иная форма 64) и длиной шнура AB. Если стрелки провеса/j и/2 не известны на разных уровнях, когда нить подвешена, но натяжение / /известно, то расстояние a и b и Стрелки провеса равны. Кроме того, разница h уровня подвески(фиг. 64 и 66): Л=А- / Р Подставьте значения J\и / 2 в это выражение согласно(6.13) и преобразуйте их с учетом a — \ — b=l: К=В1-В1=^^-А^=^Б^А^Б ^ Б-^=2л^Б- 1) Впервые эта приблизительная форма формулы Н была
указана профессором. Старман (журнал Одесского технологического института, 1925).§ 311 Откуда Гибкая нить 113 Но а — \ — в=1.、 Hh Следует отметить, что в a^>0 существует первая форма провисания для нитей(рис. 66), в<^0-вторая форма провисания и в=0-третья форма. Подставляя значения a и b в выражение (6.13), получаем значения j\и / 2: И Ф-?/2И ч ч*Н8/ / ’ 2qP2 И 2ql * 2 * Q. In в этом случае, учитывая в первом состоянии либо натяжение NY, либо провисание стрелы (зная любое из этих двух значений, уравнение (6.10) всегда может определить другое), что происходит с симметричной нитью, перекрывающейся с пролетом Z, когда температура и сила нагрузки нити после подвешивания в qt, температура нити повышается до/2 и нагрузка на длину нити равна ее пролету, а натяжение постоянно и равно N в плоской нити, эти допущения дают небольшую
погрешность. В этом случае удлинение нити накала, вызванное повышением температуры, составляет、 D$1= = a(/2-t^l, (6.16), где a-коэффициент линейного теплового натяжения материала нити накала. Когда температура повышается, нить удлиняется. В связи с этим его провисающая стрела увеличивается, в результате чего, согласно формуле (6.10), ее натяжение уменьшается. С другой стороны, с увеличением нагрузки напряжение возрастает, как видно из той же формулы (6.10). Предположим, что конечное напряжение возрастет. Тогда удлинение нити, согласно закону Гука, вызванное увеличением натяжения, равно: (Г-н х) 1-ее (6.17) 114 самостоятельный весовой учет натяжения и сжатия[Глава II. Vt. Если N*меньше N19, то значение D$2 отрицательно. При понижении температуры значение D^отрицательно. Таким образом, длина нити во втором состоянии
будет равна длине первого состояния с добавлением деформации, возникающей при повышении температуры и растяжении: D$! — /- Д$3. (6.18.) Изменение длины нити приведет к изменению и ее провисанию стрелой. Вместо F я буду / 9. Теперь заменим формулу b (6.18) и ее формулу формулой (6.11), заменив варианты D^и D$2-их значения формулами (6.16) и (6.17). Тогда уравнение(6.18) принимает вид: З(я+4^)=я(я+4?) +а^-з»)з+Т^Л/ — <6l9> В этом выражении замените значение в соответствии с выражением (6.9): 71-и=8/ / с *
Смотрите также:

