Оглавление:
Гетероскедастичность. Критерии Парка и Голдфелда — Квандта для обнаружения гетероскедастичности
При нахождении оценок коэффициентов эмпирических регрессий по наблюдениям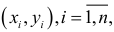 
, необходимо следить за выполнимостью предпосылок МНК, так как при их нарушении МНК может давать оценки с плохими статистическими свойствами. Одной из предпосылок МНК является условие постоянства дисперсий:
дисперсия случайной переменной 
(случайных отклонений) должна быть одинакова и постоянна для всех 
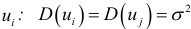для любых наблюдени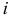й 
и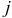 
.
Это свойство возмущающей переменной 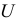называется гомокедастичностью. Непостоянство дисперсии возмущающей переменной 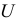называется гетероскедастичностью.
Данное условие подразумевает, что, несмотря на то, что при каждом конкретном наблюдении случайное отклонение может быть большим или маленьким, положительным или отрицательным, не может быть некой априорной причины, вызывающей большее отклонение при одних наблюдениях и меньшее — при других.
При невыполнимости данной предпосылки (при гетероскедастичности) последствия применения МНК могут быть следующими.
- Оценки коэффициентов остаются несмещенными и линейными.
- Оценки не будут эффективными (т.е. они не будут иметь наименьшую дисперсию по сравнению с другими оценками данного параметра). Они не будут и асимптотически эффективными. Увеличение дисперсии оценок снижает вероятность получения максимально точных оценок.
- Дисперсии оценок будут рассчитываться со смещением, так как дисперсия
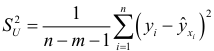не является более несмещенной. - Вследствие вышесказанного все выводы, получаемые на основе соответствующих
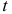— и 
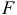-статистик, а также интервальные оценки будут ненадежными. Следовательно, статистические выводы, полученные при стандартных проверках значимости коэффициентов уравнения регрессии, могут быть ошибочными и приводить к неверным заключениям по построенной модели. Вполне вероятно, что стандартные ошибки коэффициентов будут занижены, а, следовательно, 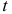-статистики будут завышены. Это может привести к признанию статистически значимыми коэффициентов, которые таковыми не являются.
Для обнаружения гетероскедастичности применяются различные методы: графический анализ отклонений, критерии ранговой корреляции Спирмена, Парка, Глейзера, Голдфелда — Квандта.
Рассмотрим критерий Парка. Предположим, что дисперсия отклонений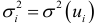 
является функцией 
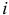-го значения 
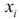факторного признака, которая описывается функцией 
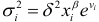, где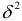 
— неизвестная константа. Прологарифмировав эту функцию, получим 
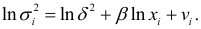. Так как дисперсии 
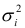неизвестны, то их заменяют оценками квадратов отклонений 
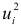. Применение критерия Парка включает следующие шаги.
- Строится уравнение регрессии
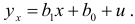
- Для каждого наблюдения определяются
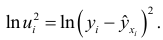
- Строится регрессия
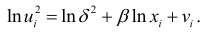
В случае множественной регрессии зависимость (4.1) строится для каждого факторного признака.
Проверяется статистическая значимость коэффициента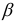 
уравнения (4.1) при помощи статистики 
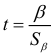. Если коэффициент 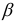статистически значим, то это свидетельствует о наличии связи между 
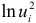и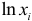 
, т.е. о наличии гетероскедастичности в эмпирических данных.
Критерий Голдфелда — Квандта. Предположим, что дисперсия отклонений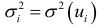 
является функцией 
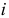-го значения 
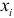факторногпризнака, которая описывается функцией 
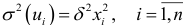возмущающая переменная имеет нормальное распределение и отсутствует автокорреляция остатков 
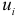. Критерий Голдфелда — Квандта состоит в следующем:
- Все
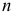наблюдений упорядываются по величине значений фактора 
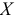. - Упорядоченная выборка разбивается на три подвыборки объема
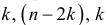. - Строятся уравнения регрессии для первой и третьей подвыборок. Если предположение о пропорциональности дисперсий отклонений значениям 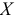верно, то дисперсия регрессий по первой подвыборке,
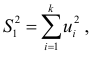будет существенно меньше дисперсии регрессии по третьей подвыборке,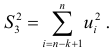 
- Для сравнения дисперсий составляется 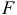-отношение:
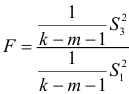, которое подчиняется 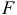— распределению с числом степеней свободы 
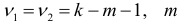— количество факторных признаков в уравнении регрессии. - Если
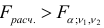, то гипотеза об отсутствии гетороскедастичности отклоняется. В противном случае, т.е. если 
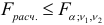, нет оснований для отклонения гипотезы о гомоскедастичности остатков.
Голдфелд и Квандт для парной регрессии предлагают следующие размеры подвыборок: если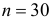 
,то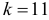 
; если 
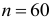, то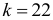 
.
При множественной регрессии данный критерий применяется для факторного признака с найбольшей дисперсией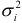 
или для всех факторных признаков.
Критерий Голдфелда — Квандта можно применять и при обратной пропорциональной зависимости между 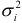и значениями факторного признака.
Пример 4.1.
По эмпирическим данным, описывающих величину потребления (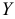
, ден. ед.), в зависимости от величины дохода (
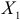, ден. ед) и инвестиций (
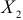, ден.ед.):
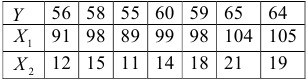
построить линейную регрессионную модель и проверить случайность остатков.
Решение. Линейная регрессионная модель зависимости объема потребления от величины дохода и инвестиций имеет вид:
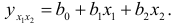
Коэффициенты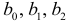 
неизвестные величины. Определим их при помощи МНК. Применив ЭВМ, находим уравнение регрессии:
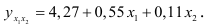
Подставив в полученное уравнение регрессии значения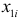 
и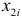 
вычисляем значения регрессии 
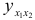и остатки 
:
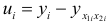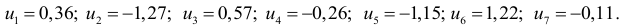
Случайность остатков проверим при помощи критерия серий. Для этого образуем последовательность из плюсов и минусов по следующему правилу: если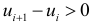 
, то ставится плюс; если 
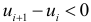, то ставится минус. Для вычисленных остатков получаем следующую последовательность знаков:
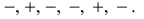
Общее число серий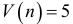 
и протяженность самой длинной серии 
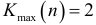. Подставив эти значения в неравенстве
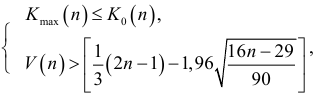
получим 2<5, где
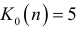
для
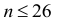
и
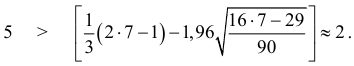
Следовательно, отклонения от уравнения регрессии носят случайный характер.
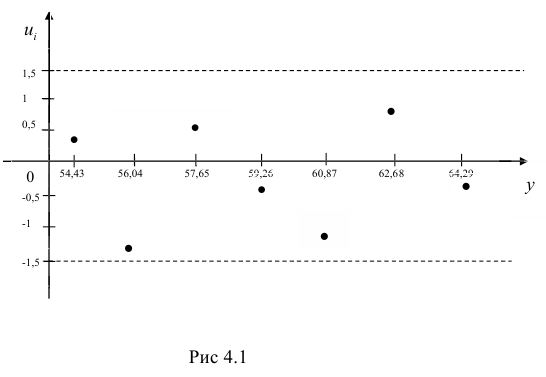
Проведем графический анализ зависимости остатков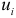 
от теоретическихзначений результативного признака 
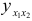. Для этого построим на графике (рис. 4.1) значения отклонений. Поскольку точки находятся в полосе, обозначенной пунктирными линиями, то отклонения носят случайный характер и, следовательно, уравнение регрессии хорошо аппроксимирует изучаемое явление.
Эта лекция взята со страницы предмета «Эконометрика»
Предмет эконометрика: полный курс лекций
Эти страницы возможно вам будут полезны:
