Геометрическое представление движения по Пуансо

Оглавление:

Геометрическое представление движения по Пуансо

В работе, опубликованной в XVI Journal de Liouville, пуансетто дал геометрическое представление движения, основанное на следующей теореме кинематики, которая справедлива в любом случае движения твердого тела вокруг неподвижной точки. Рассмотрим эллипсоид инерции тела, построенный с фиксированной точкой O, к OX. О, о главная ось инерции этого ellipsoid. В какой то момент времени ось вращения Ош пересекается с поверхностью эллипсоида в определенной точке М. Это называется полюс.

Теорема Кинетическая энергия тела 2 0 На самом деле, исходя из самого определения эллипсоида Момент инерции Тело относительно оси Ош равно= , от Причем скорость точки объекта такова, как если бы объект вращался с угловой скоростью w вокруг Ош, поэтому кинетическая энергия j then2 равна половине произведения момента инерции. Квадрат угловой скорости пункт 359 Теорема II в каждый момент времени касательная плоскость эллипсоида инерции на полюсах m перпендикулярна основному моменту ОА импульса. Фактически, эллипсоид инерции относится к оси Oxyz Есть такое уравнение. Ax2 By2 Cz2 =.

Эта теорема, которой мы уже пользовались, интересна кроме прочего и в том отношении, что она придает реальное значение теории движения материальной точки. Людмила Фирмаль

Косинус направления вектора Ош равен, , , и координатам Р полюс Т Можно представить себе по отношению к одной и той же оси Х = ом г = От, р = от. В результате уравнение касательной плоскости в точке m x, y, r AXxBY y Czz = I Принимать форму ApX BqY CrZ = 1. Эта плоскость перпендикулярна вектору Oa, где проекция равна Ap, Bq, Cr. Теорема III расстояние от неподвижной точки до плоскости, касательной к эллипсоиду инерции полюса, равно квадратному корню из 2x кинетической энергии, деленному на главный момент импульса. Фактически, расстояние от точки O до касательной плоскости От VA2p2+ BV + Это доказывает теорему.

Здесь мы применяем эти 3 теоремы к частным случаям, когда сила, приложенная к твердому телу, уменьшается до одного результата, который проходит через неподвижную точку. Следующий 1.Кинетическая энергия постоянна и равна L или Ots2.Поэтому мы имеем = = 0. 2.Основной момент импульса направление ОА фиксируется. Плоскость, касательная к эллипсоиду в точке m, также фиксирует направление, перпендикулярное Oa. 3.Основной момент ОА имеет постоянное значение 1, или расстояние от точки О до касательной плоскости, например 1 по. Равный 8 i Vd также является постоянным.

В результате плоскость, касательная к точке М, становится неподвижной, так как она имеет определенное направление и находится на определенном расстоянии от неподвижной точки О. Поэтому мы пришли к выводу, что инерционный эллипсоид всегда касается неподвижной плоскости P. точка соприкосновения m Полюс, прямая линия от это мгновенная ось, а мгновенная угловая скорость w, равная OT n, пропорциональна от. Пуансетто называет кривую, описываемую полюсом m на поверхности эллипсоида, породой, а хелполоди называют кривую, описываемую полюсами на неподвижной плоскости II рис.228.Конусы являются геометрическим локусом мгновенной оси тела и имеют вершины Рисунок 228.

В точке O, как направляющая, половина длины конус это геометрическое расположение мгновенной оси в пространстве, имеет вершину в точке O и имеет вспомогательную ось в виде base. To чтобы получить движение, нужно повернуть первый конус вдоль второго так, чтобы мгновенная угловая скорость u была пропорциональна At в каждый момент времени. и = о л л. Точка эллипсоида в контакте с плоскостью Р обусловлена тем, что она всегда имеет скорость, равную нулю.

Поскольку он находится на мгновенной оси, также можно: Условия. Когда эллипсоид инерции вращается без скольжения вдоль неподвижной плоскости P, происходит движение. Этой неподвижной плоскости Роли и должности Если предположить, что поверхность катящегося конуса практически ограничена половиной его длины, то можно представить себе движение и по другому. Сформированный таким образом объект катится по плоскости Р, и его последующее движение является подспорьем рис. 228А. Длины соответствующих дуг обеих кривых одинаковы, поскольку полуполюсы не скользят и не вращаются вдоль изоляции. 228А. Он полон. Найдите уравнение потопа. Для этого мы назначаем его оси эллипсоид инерции.

Породи можно определить как траекторию точки m , y, r эллипса. Ахх Баю Зчз = Находится на некотором расстоянии 8 = =от начала координат. Это условие выражается следующим уравнением Lx2 + B2 C22r = O. 29 Это уравнение объединено с уравнением эллипсоида Ax2 + + Cr2 = 1 30 определяет polody. So это кривая алгебры 4 го порядка. Форма этой кривой может быть представлена как пересечение эллипсоида и cone. An эллипсоид и конус это геометрические положения мгновенной оси вращения от в теле, или то же самое, то есть вращающийся конус.

Уравнение этого конуса получается путем удаления правой части из уравнений 29 и 30, а уравнение А А Д ХВ + Б Б Д Йи + с С Д Зи = о Для того, чтобы этот конус был реальным, необходимо л о С. Это четкое условие, что расстояние от касательной плоскости до начала координат должно быть меньше максимального Половинный вал Больше минимальной оси D =.Кукуруза вы в а Если D = A или D = C, то это прямая линия, которая совпадает с осью Ox или Oz и рождается в 2 виртуальных плоскостях. Это можно легко объяснить геометрически. Это связано с тем, что конец длинной оси a является только концом c, а c является концом короткой оси a и A. 1. центр эллипсоида и главная плоскость.

Каждая ветвь имеет плоскость Симметрия это другие 2 главные плоскости эллипсоида рис. 229, которые имеют 4 вершины, 2, 1, 2, и радиус вектор O, выходящий из центра, максимизирован или minimized. As вы двигаетесь, 1 из ветвей породы будет вращаться вдоль неподвижной плоскости P. используется только эта ветвь. 2 я ветвь вращается вдоль плоскости, симметричной II относительно точки O. В зависимости от начальных условий важно распознавать различные формы затопления. Представьте эллипсоида инерции рис. 229. Поскольку мы предполагаем, что L B C, ось Ox является малой осью, а Oz большой осью. предположим, что A, a , b, b , c, c обозначает вершину поверхности.

В зависимости от начальных условий константа D изменяется от A до C. In D A, конус это геометрическая траектория момента Ось вращения тела вырождается в ось Ox, а полуволна пересечение этого конуса и эллипсоида вырождается в точку div, точку симметрии точки a. При незначительном уменьшении D полупериод состоит из небольшой замкнутой кривой, охватывающей a, и симметричной кривой, охватывающей. Если D продолжает уменьшаться, то кривые f и f удаляются от a и d, а если D = B, то эти кривые соединяются точками b и b и делятся на 2 эллипса e и e .Аналогично, при D = C полулиния вырождается до 2 пиков c и c.

Если вы увеличите D, линия наводнения первоначально будет состоять из 2 небольших симметричных замкнутых кривых g и g , которые окружают эти вершины. Эти кривые увеличиваются, и при D = B они снова превращаются в эллипсы e и E. Поэтому существует 2 вида затопления. Некоторые из них окружают вершины малой оси, а другие большой оси. Эти 2 типа пород разделены специальной породой, соответствующей D = B, и образованы двумя эллипсами e и e .Существует только 1 порода, проходящая через каждую точку поверхности эллипсоида.

Если все эти кривые уже вычерчены, то зная точку m0, в которой ось начального мгновенного вращения пересекает эллипсоид, достаточно выяснить, какой пород соответствует заданному начальному условию. Желаемый поток это поток, который проходит через m0.Соответствующая неподвижная плоскость P. As для плоскости это плоскость, которая касается эллипсоида в исходном положении. Хелплодия. Когда перпендикулярная линия опущена из неподвижной точки Длина плоскости II рис. 228 или, следовательно, или Равный Вектор Pm = p для некоторых точек справки. Радиус Есть длина Основываясь на форме наводнения, мы видели его distance. It варьируется от полюса к центру, от минимума до максимума.

Таким образом, P также варьируется между соответствующими минимальными и максимальными Пи. Таким образом, helpolodia заключена между 2 концентрическими окружностями радиуса p и p2, которые последовательно соприкасаются в таких точках, как m и t2.It имеет форму, показанную на рисунке 228.Это кривая, которая всегда имеет вогнутую поверхность по направлению к точке P и не имеет точки перегиба. Эта ситуация была впервые замечена Гессом трактат, Мюнхен, 1880 mathematics Annalen, Vol. XXVII , а спаррер был вновь открыт dosparais, conteslendus, 1884, придав ему форму синуса. Доказательство находится в статье паде Pad4, Nouvelles Annes, 4 s4rie, vol. VI, 1906 7.

Центр тяжести системы, движется как материальная точка, масса которой равна всей массе системы и к которой приложены силы, равные и параллельные внешним силам системы. Людмила Фирмаль

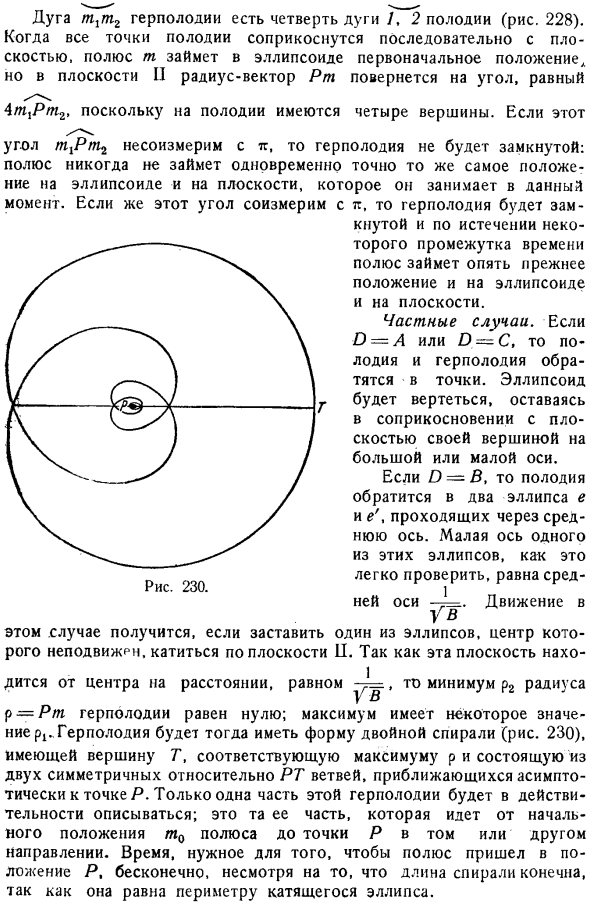
Дуга mtm2 helpodia составляет 1, 2 и 1 4 дуги polodi рисунок 228.Если все точки полулинии расположены последовательно с плоскостью. В то время как полюс m занимает начальное положение эллипсоида, в плоскости II радиус вектор Pm поворачивается на следующий угол. 4m Ptr, потому что на полулинии есть 4 вершины. Вот этот. Поскольку угол n Pm не может быть разрешен с этим, helpodia не закрывается. Полюс не будет занимать точно такое же положение в то же время на плоскости, в настоящее время занятой эллипсоидом. Если этот угол пропорционален ему, то опора закрывается, и через некоторое время полюс снова занимает то же положение на овале в плоскости. Особый случай.

Если = A или D C, то halftime и harpodium изменятся на точки. Эллипсоид будет вращаться, и его вершины будут оставаться в контакте с гранью на длинной или короткой оси. В случае D B полупоток превращается в 2 эллипса e, проходя через среду. чтобы было легче проверить, малая ось 1 эллипса равна средней оси r=.Движение В Если получится, сверните 1 овал с неподвижным центром вдоль плоскости I. Так как эта плоскость находится на расстоянии от центра, то минимальное значение радиуса P2 =Pt хеллполоды равно нулю. Наибольшее значение p. helpodia будет иметь форму двойной спирали рис.

Где вершина T соответствует максимуму p и состоит из 2 ветвей, симметричных PT, асимптотически приближающихся к точке P. фактически записана только часть этой helpodia. Это отрезок от начального положения n0 полюса в ту или иную точку P. Несмотря на то, что Длина спирали конечна, время, необходимое полюсам для достижения положения P, бесконечно, так как полюса равны окружности вращающегося эллипса. Если эллипсоид является сфероидом, то полукруг и справка это круги. Если это сфера.

Наводнение и холод всегда будут иметь значение. Стабильность вращения вокруг основной оси axis. In в особых случаях, когда тело начинает вращаться вокруг 1 главной оси инерции, такие вращательные движения продолжаются бесконечно. Мгновенная ось перестает двигаться в теле и space. It легко видеть, что только в них мгновенная ось остается неподвижной в пространстве. body. In факт, мы предполагаем, что мгновенная ось не движется в теле, это обозначается a, B.

Используйте направляющий Косинус для осей Oxyz. У нас есть п = Где A, B и C являются константами. Интеграл кинетической энергии 12 показывает, что постоянна. Таким образом, 3 компонента p, q, r становятся постоянными, а уравнения Эйлера принимают вид: Если эллипсоид инерции не является сфероидом, то из этих уравнений видно, что 2 величины p, q и r равны нулю, то есть тело вращается вокруг главной оси инерции. Если эллипсоид представляет собой сфероид Оз вокруг оси, то либо A = B и r = 0, и тело вращается вокруг оси. На экваториальной плоскости, то есть вокруг главной оси инерции, или p = q = 0, тело вращается вокруг главной оси Oz.

Наконец, если A = B = C, то тело вращается вокруг главной оси инерции, так как все оси являются главной осью. Теперь вопрос заключается в том, является ли вращение объекта вокруг 1 из этих главных инерционных осей устойчивым движением. Кроме того, в общем случае говорят, что движение устойчиво, если минутные изменения самого движения соответствуют любым минутным изменениям начальных условий. Движение называется неустойчивостью, когда незначительное изменение начальных условий сопровождается конечным изменением движения. Для a B C вращение вокруг большой и малой осей эллипсоида инерции является стабильным, а вращение вокруг промежуточных осей является unstable.

Дело в том, что он сигнализирует телу о начальном вращении вокруг короткой оси. Тогда эта ось остается неподвижной, полюса вращения совпадают с вершиной a, а касательная плоскость Po точки Oo становится неподвижной. Здесь, придавая телу начальное вращение вокруг оси, бесконечно близкой к Oa0, изменяя минутное начальное условие, породи превращается в небольшую замкнутую кривую, бесконечно близкую к вершинам малой оси. Таким образом, мгновенная ось, вокруг своего начального положения, представляет собой конус с минимальным углом решения его телом.

Фиксированной поверхности ти Эллипсоид вступает в контакт с новым движением, становится бесконечно близким к ПО, а величина и положение перпендикуляра ОП, отброшенного С О на эту плоскость, бесконечно близки к ОД. Радиус вектор от герполоды, длина которого близка к бесконечности до Ойо, бесконечно мало отклоняется от перпендикуляра ОП, т. е. Oa0.As в результате мгновенная ось также представляет собой конус, бесконечно близкий к своему исходному положению в пространстве. space. So вращение задачи стабильно. То же самое происходит, если вы вращаетесь вокруг главной оси.

Однако если тело сначала начинает вращаться вокруг центральной оси, то незначительное изменение начальных условий приводит к перемещению полюсов в положение f o, из которого описываются породы, окружающие вершину a или вершину c. Тогда ось отклоняется на конечное значение от своего первоначального положения. Вращение становится неустойчивым. Его Эллипс и e e рис. 229 делят эллипсоид на 4 части.2 содержит вершины A и A , а другие 2 содержит вершин C и C. Следуя замечаниям Бура, естественно принять отношение половины площади к половине площади инерционного эллипсоида в качестве меры устойчивости вращения вокруг ОА axis.

Дело в том, что если начальные условия изменяются так, что полюса находятся в этой части, то мгновенная ось представляет в теле конус вокруг его начального положения ОА. Аналогично, стабильность вращения вокруг оси измеряется площадью детали, содержащей эту ось. Например, если эллипсоид очень близок к сфероиду вокруг Oz, то есть если A B очень мал, то часть, которая содержит a. Is очень мало, потому что полюса выходят из этой части при небольшом смещении оси и вращаются вокруг ОС, поэтому устойчивость вращения вокруг ОА ослабляется.

Если эллипсоид это точно сфероид удлиненный снаряд, то только вращение вокруг оси симметрии stabilizes. In дело в том, что если тело вращается вокруг 1 главной оси экваториальной плоскости, а в некоторых случаях полюса м слегка отклоняются от этой плоскости, то на поверхности эллипсоида рисуется окружность, параллельная экватору и примерно совпадающая. При слиянии ось тела сильно отклоняется от своего первоначального положения. Заметим, что в пространстве ось, наоборот, остается очень близкой к исходному положению, так как длина от почти совпадает с экваториальным радиусом.

Случай, когда эллипсоид инерции является эллипсоидом вращения	Уравнение герполодии
Краткие указания к вычислению девяти косинусов в функции времени	Интегралы, получаемые из общих теорем

Если вам потребуется заказать теоретическую механику вы всегда можете написать мне в whatsapp.