Геометрическое изображение комплексных чисел
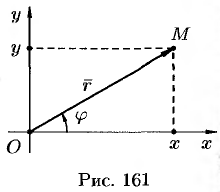
Всякое комплексное число 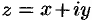 можно изобразить точкой
можно изобразить точкой 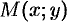 плоскости
плоскости 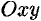 такой, что
такой, что 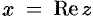 ,
, 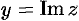 . И, на-
. И, на-
оборот, каждую точку 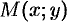 координатной плоскости можно рассматривать как образ комплексного числа
координатной плоскости можно рассматривать как образ комплексного числа 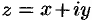 (см. рис. 161).
(см. рис. 161).
Плоскость, на которой изображаются комплексные числа, называется комплексной плоскостью. Ось абсцисс называется действительной осью, так как на ней лежат действительные числа 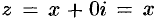 . Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа
. Ось ординат называется мнимой осью, на ней лежат чисто мнимые комплексные числа 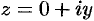 .
.
Комплексное число 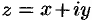 можно задавать с помощью радиус-~ вектора
можно задавать с помощью радиус-~ вектора 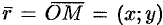 . Длина вектора
. Длина вектора 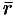 , изображающего комплексное число
, изображающего комплексное число 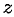 , называется модулем этого числа и обозначается
, называется модулем этого числа и обозначается 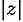 или
или 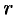 . Величина угла между положительным направлением действительной оси и вектором
. Величина угла между положительным направлением действительной оси и вектором 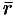 , изображающим комплексное число, называется аргументом этого комплексного числа, обозначается
, изображающим комплексное число, называется аргументом этого комплексного числа, обозначается 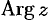 или
или 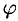 .
.
Аргумент комплексного числа  не определен. Аргумент комплексного числа
не определен. Аргумент комплексного числа 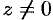 — величина многозначная и определяется с точностью до слагаемого
— величина многозначная и определяется с точностью до слагаемого 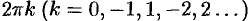 :
: 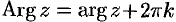 , где
, где 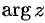 — главное значение аргумента, заключенное в промежутке
— главное значение аргумента, заключенное в промежутке 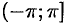 , т. е.
, т. е. 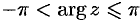 (иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку
(иногда в качестве главного значения аргумента берут величину, принадлежащую промежутку 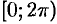 ).
).
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Формула Тейлора для многочлена |
| Формула Тейлора для произвольной функции |
| Формы записи комплексных чисел |
| Действия над комплексными числами |

