Геометрическое истолкование инварианта

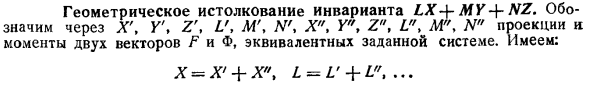
Геометрическое истолкование инварианта

• ВХ + му + Н2. X , Y X , L , M , X , Y , 2, a , L1, I проекция и 2 вектор P и моментов, соответствующих определенной системе. Ранее установлено о взаимных моментах 2 векторов С. 12 рассматривая формулу, она выглядит так: ДХ 4 4 = Д 4 Д Х 4 Х 4… = 6 объем. Л Ф это позволяет получить замечательную геометрическую интерпретацию инвариантов DX4 L4U4 LG2. П2…Р2 начальный вектор предлагаемой системы. У нас есть отношения. Д. = … 1 1кхк + МКУК + 2К = о 2.

Необходимо показать, что шесть деле, присоединение или отбрасывание приложенным в не изменяются. Людмила Фирмаль

Отношения 1 и идентичность 2 Спасибо ЛК + МУ + Н2 = я Л ХК + м, Ык + шк + 1kX + м МКУ + а 2. Здесь сумма правых распространяется на все попарные комбинации индекса I и k, но выражение под знаком 2 является обратным моментом вектора и Pk. ДХ4 Л1У4 = е объем. Р6Рк Вот количество терминов во 2 м члене: вектор Pk шаль combination. In для того чтобы метки помещали 2 вектора P и в одну плоскость, необходимо и достаточно, чтобы объем Шариатетраэдра был равен нулю.

• Покажем теперь, что оба указанных элементарных действия не изменяют ни главного вектора, ни главного момента относительно произвольной, точки. Отбрасывание в каждой сумме двух слагаемых, равных по величине и противоположных по знаку моментов этих векторов — моментом равнодействующего вектора в последних трех суммах указанных сумм.

Существует бесчисленное множество способов приведения заданной системы векторов к двум векторам. Людмила Фирмаль

Система скользящих векторов может быть заменена бесчисленным множеством способов двумя векторами, из которых один проходит через произвольную точку. указанные прямые образуют триэдр. Эти три вектора можно привести к двум. Таким двум векторам, из которых Ъдин лежит на произвольной прямой, не параллельной главному вектору. Рп — первоначальные векторы предложенной системы. систем друг к другу.

Смотрите также:

Предмет теоретическая механика

Элементарные операции	Приведение двух эквивалентных систем друг к другу
Приведение к двум векторам	Пары