Оглавление:


Геометрический вывод
- Геометрические рассуждения. Вывод формулы(6)можно построить, следуя Остроградскому, и по чисто геометрическим соображениям[ср.Н°355]. Бесконечно малый кубоид в пространстве CA с размерами 6Y, yt] отображается на основное тело в пространстве
объятий между координатными поверхностями » B » и «Tr>and»?]С -^», «С»и это можно грубо рассматривать как косой параллелепипед. Его объем равен объему тетраэдра с вершиной в точке:^1 (L>Y>*),^2Y~y g4»> г+5yy+^гг+П</(:)’
И согласно формуле, известной из аналитической геометрии, она представляется (в абсолютном Людмила Фирмаль
значении) определителем^X , ~д^< _R (х,у,Г)О (&, Ч,Ы) После (а).& Если суммировать эти отдельные»элементы объема», то получится выражение (6). Итак, суть задачи здесь заключается в том, что для определения объема тела необходимо определить элементы не по системе плоскостей, перпендикулярных друг другу, а по сетке
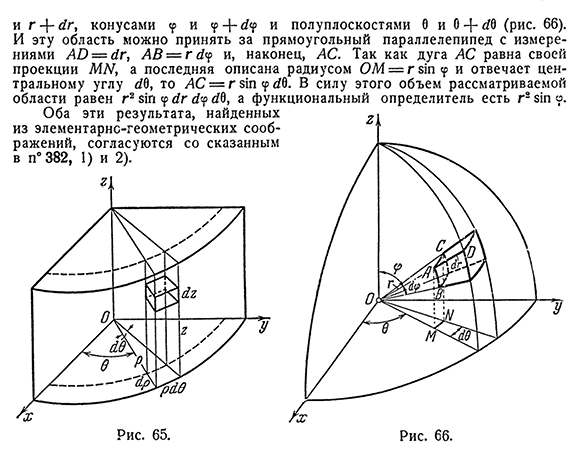
координатных плоскостей. Например, C и l и L и N d R и h E s K и x K o R d и n a t разбиты двумя цилиндрическими гранями радиуса p и p+^P 65). Если рассматривать эту область приблизительно как прямоугольный параллелепипед, то ее размеры составляют b / R, p<70, YG, объем которого равен p y yg, и отношение этого объема к объему B/R b/V YG. Аналогично, в случае f E R и h E s K и x K o R d и n a t, число XXIII. тройной интеграл [385], рассматривающий основную область
- (пространство объятий), окруженную сферой радиуса g352 И Г-Б/г, конус<? И полуплоскости 0 и 0 — ^6(рис. 66). И эту область можно принять за прямоугольный параллелепипед с размерами=AV-Gyu, и
наконец. Поскольку дуга AC равна ее проекции, а последняя описывается радиусом OM-Gy PU, и соответствует центральному углу b/0, то AC-g81p<? b / 0 по этой причине объем рассматриваемой области равен G2at<? Ю. Г. Ю. Б /
0, и функциональный определитель Людмила Фирмаль
G2ZYU часов. Оба эти результата, полученные из основных геометрических соображений, согласуются с тем, что было сказано Райс, 66. n°382, 1) и 2).
Смотрите также:
Решение задач по математическому анализу
| Преобразование пространственных областей. | Случай произвольного промежутка |
| Выражение объема в криволинейных координатах. | Полнота тригонометрической системы. |

