Геометрический вывод

Оглавление:

Геометрический вывод

Геометрические рассуждения. Формула силы есть еще одна производная от этой формулы, которая, хотя и проста, но не N GL I d n s x, совершенно прозрачна с геометрической стороны;она принадлежит Остроградскому[n°359]. Рассмотрим еще раз

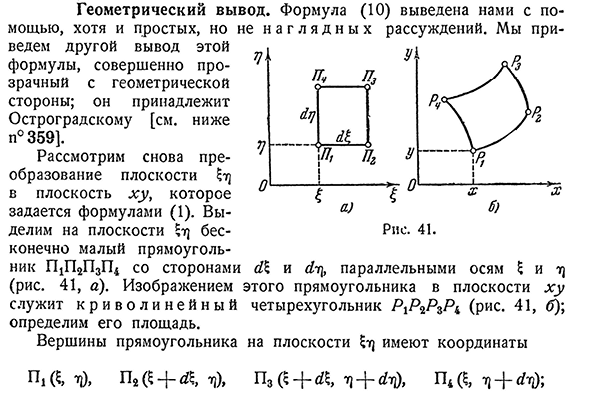
преобразование плоскости в плоскость XY, заданную Формулой(1). Выделите бесконечно малый прямоугольник P1P3P4 с его сторонами на плоскости(рис. 41, а). Изображение этого прямоугольника в плоскости XY, четырехугольника R^R^R^(рис. 41, b);

определите эту область. Вершины прямоугольника на плоскости имеют координаты Людмила Фирмаль

В, параллельно оси H 7) п н е, т}), Р2(? +^, Т]), Р3(х+г е 7 1+^7]), Р4(е, 7)+^;284CHAP. Двойной Интеграл[355 В этом случае соответствующая вершина четырехугольника кривой имеет следующие координаты: P1 (•*&»P),^(5,■»!)что случилось? Л(Х(5+<г, 7)), г(? + < / ?, 7]), л(х o~Б»г^7])>у~{~^71))>Р4(^0,+^)>у&»>1+^)). Если мы ограничимся первичным членом по отношению к (1), мы можем взять точку: p R и b l и f e n o: A

(Xy\^2<&>Y+ , Где x=x ( $ , 7]), y=x ( % , t]) и, в общем случае, все производные вычисляются с помощью(B, t]). Поскольку проекции на сегменты PXR2 и обе оси равны, соответственно, эти сегменты одинаково параллельны, поэтому меньшие, более высокого порядка четырехугольники P^R^R^r^r^r^. Его площадь равна площади вдвое большей площади треугольника P^P^. Из геометрии анализа

известно, что площадь удвоения треугольника, где вершины находятся в точках (XH (x2, _u2), (X3, y3), равна b C O L y t o y E l и h и N e. U2-U uz-u2 ‘ если применить эту формулу к нашему случаю, то можно увидеть, что область интереса (опять—таки-небольшая область с более высоким порядком) равна Б О Л У Т н о й е л и ч и н е. * DH. О(Х, Y)) Так… , Проксированный P^R^r y=/Y71-разложить фигуру (D) на плоскости W] прямой s m I, p A R a l l l l l l l l на оси, в бесконечно малый прямоугольник (и игнорировать»неправильный»элемент

контура), заменив переменную в двойном Интеграле 285. т ы р е х у Г О Л Ь Н И К и мыслимых видов. Суммируя полученную формулу для этих областей, мы снова приходим к формуле (*).Десять.) Сделать такой вывод нетрудно. **) Мы предполагаем, следовательно, наличие и непрерывность смешанных производных вторичных и также. См. сноски на стр. 279. Суть Формулы (10) заключается в том, что для определения площади фигуры (Р) эту фигуру не разлагают на традиционные прямоугольные элементы

, используя сетку прямых линий, параллельных оси.- Два луча, исходящие из Использование Людмила Фирмаль

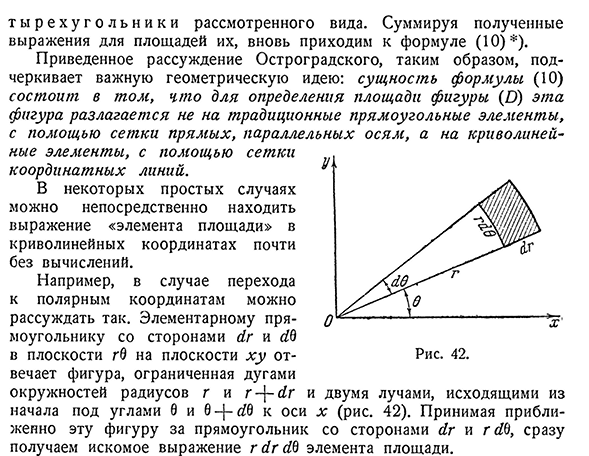
сетки координатных линий, элементов. В некоторых простых случаях можно непосредственно найти представление «элементов области»в криволинейных координатах с небольшим или вообще без расчета. Например, в случае перехода к полярным координатам можно так рассуждать. Основной прямоугольник XY со сторонами YG и M плоскости G9 на плоскости соответствует фигуре, ограниченной дугой окружности радиусов g и g^ — YG под углами 9 и 9 — / — ^K o si x (рис. 42). Возьмите эту цифру примерно на прямоугольник из сторон YG и г< / 9 и сразу же получить нужные представления квадратный элемент Г. Ю. Г. Ю.

Выражение площади в криволинейных координатах.	Замена переменных в двойных интегралах
Дополнительные замечания	Аналогия с простым интегралом. Интеграл по ориентированной области