Геометрический смысл производной.

Геометрический смысл производной

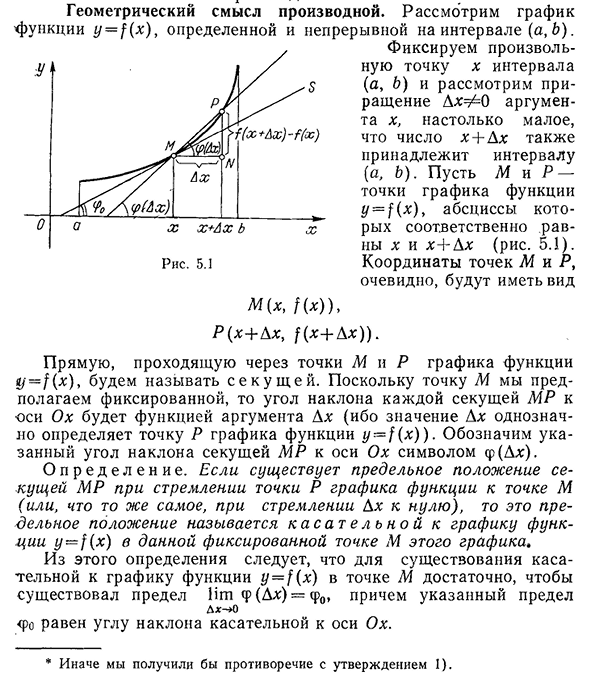
• Геометрический смысл производных. Рассмотрим график функции y=} (x), которая определяется интервалом (a, B) и является непрерывной. Зафиксируйте любую точку x в интервале (a, B) и рассмотрите приращение DX= # =0 в аргументе x, сделайте число x+DX

меньшим, чтобы оно также принадлежало интервалу (a, B). Пусть M и P-точки графа с функцией y=1 (x), абсцисса которой равна x и X+DX соответственно(рис. 5.1). Координаты точек M и P явно принимают следующий вид М(ч, ч)), р (ч+ЛГ,|(х+D х)).

Линии, проходящие через Людмила Фирмаль

точки M и P на графике функции, называются секущими. Поскольку точка M считается фиксированной, наклон каждого секущего Mr к его оси становится функцией аргумента DX(значение DX однозначно определяет точку P графика функции g/=/(x) как заданный наклон секущего Mr к символу кванта ox<p (DX)). Если точка P в графе

функции стремится к точке M (или, если она одинакова, DH стремится к нулю), то эта предельная позиция равна заданному фиксированному значению этого графа. Из этого определения следует, что для наличия касательных к графу функции y=(x) в точке M достаточно иметь предел NT<p (DX)=<P0,а указанный предел DX-

• «o<ro». В противном случае это противоречит утверждению 1).§2. Понятие Дифференцируемости функции 193 Докажем следующее утверждение -. Если функция y=HX) имеет производную в заданной неподвижной точке x, то касательная к графу функции y-CX находится в точке M (x, 1 (x)), а угловой коэффициент этой касательной (то есть угол к оси ox). Из точек M и P опустим перпендикуляр к оси абсцисс (см. рисунок). 5.1). Нарисуйте линию точки M, параллельную оси X, и

обозначьте пересечение этой линии и перпендикуляра от P по оси x на N. из треугольника MKR ясно \&Щ(х+Ах) — г(х) Ф (Ах)=-^ = Л — — DH. И так оно и есть., Ф(Ах)=ags1 (5.6) DH. Давайте убедимся, что существует предел правой (и, следовательно, левой) части (5.6) в DX — * 0. Фактически, существование производной/'(x)ограничивает ее-^-=/'(x). Следовательно, и от ДХ — » о, ДХ

Непрерывность функции AGS (§и для всех значений правая часть (5.6) будет иметь предел, равный Людмила Фирмаль

ags1§//(x). Итак, мы доказали, что существует предел NT f(DH) = agc1§(x). ДХ — » 0″ То есть существует касательная к графу функции в точке L4 (x,/(x)), а наклон касательной к оси ox равен fo=ags1§ § / ‘(x). Таким образом, угловой коэффициент указанного касательного 1§F0 равен/'(x). Сформулированное предложение доказано.

Смотрите также:

Методическое пособие по математическому анализу

Определение производной	Первообразная
Второе достаточное условие экстремума	Дифференциалы высших порядков