Геометрический способ сложения сходящихся сил
Системой сходящихся сил называется система сил, линии действия которых пересекаются в одной точке (рис. 15,а). Если мы перенесем все силы такой системы но линиям их действия в общую точку пересечения этих
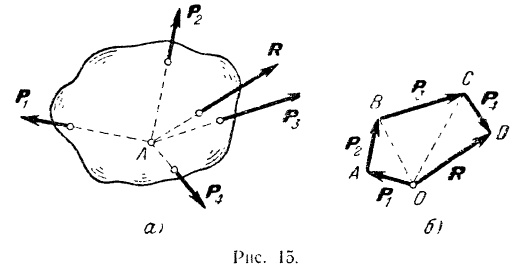
линии, то, согласно первому следствию из аксиом статики, действие системы на абсолютно твердое тело не изменится. Таким образом, любую систему сходящихся сил можно заменить эквивалентной системой сил, приложенных в одной точке.
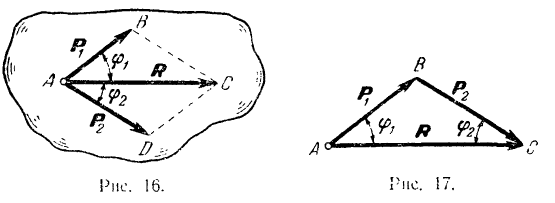
Задача о сложении двух сил, приложенных к одной точке, геометрически решается построением соответствующего параллелограмма сил (рис. 16) или силового треугольника (рис. 17), изображающего одну из половин параллелограмма.
Для построения силового треугольника из конца вектора одной силы 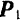 проводим вектор
проводим вектор 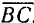 , изображающий вторую силу
, изображающий вторую силу 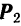 . Замыкающая сторона
. Замыкающая сторона 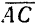 треугольника изображает но модулю и по направлению равнодействующую
треугольника изображает но модулю и по направлению равнодействующую 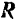 двух данных сходящихся сил.
двух данных сходящихся сил.
Последовательно применяя правило треугольника, можно найти равнодействующую любого числа сходящихся сил, например четырех сил 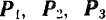 и
и 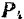 (рис. 15, а). Для этого из_произвольной точки
(рис. 15, а). Для этого из_произвольной точки 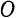 (рис. 15,6) отложим вектор
(рис. 15,6) отложим вектор 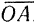 , изображающий в принятом масштабе силу
, изображающий в принятом масштабе силу 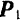 , из конца его— вектор
, из конца его— вектор 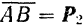 , из его конца — вектор
, из его конца — вектор  и т. д., помещая всякий раз начало следующего вектора в конце предыдущего, пока не исчерпаем все силы.
и т. д., помещая всякий раз начало следующего вектора в конце предыдущего, пока не исчерпаем все силы.
Полученный многоугольник 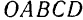 , стороны которого в выбранном масштабе равны модулям составляющих сил и одинаково с ними направлены, называется силовым многоугольником.
, стороны которого в выбранном масштабе равны модулям составляющих сил и одинаково с ними направлены, называется силовым многоугольником.
Очевидно, что равнодействующая 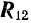 сил
сил 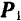 и
и 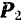 изображается (рис. 15,6) вектором
изображается (рис. 15,6) вектором 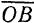 , равнодействующая
, равнодействующая 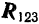 сил
сил 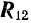 и
и 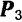 изображается вектором
изображается вектором 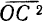 ) и замыкающая сторона
) и замыкающая сторона 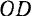 силового многоугольника, направленная от начала вектора первой силы к концу вектора последней, изображает в выбранном масштабе равнодействующую данной системы сходящихся сил (т. е. сил
силового многоугольника, направленная от начала вектора первой силы к концу вектора последней, изображает в выбранном масштабе равнодействующую данной системы сходящихся сил (т. е. сил 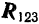 и
и 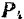 ) как по модулю, так и по направлению.
) как по модулю, так и по направлению.
Правило сложения сходящихся сил по способу многоугольника является общим правилом сложения любых векторов и называется их геометрическим сложением.
Геометрическая сумма всех сил любой системы называется главным вектором 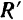 этой системы
этой системы
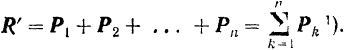
Таким образом, можно сказать, что равнодействующая 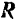 системы сходящихся сил проходит через общую точку пересечения линий действия этих сил и равна по модулю и направлению их главному вектору.
системы сходящихся сил проходит через общую точку пересечения линий действия этих сил и равна по модулю и направлению их главному вектору.
Геометрическая сумма векторов не зависит от перемены мест слагаемых и, следовательно, при изменении порядка сложения сил их главный векгор не изменяется.
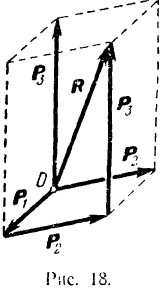
В частном случае трех сходящихся сил 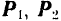 и
и 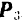 не лежащих в одной плоскости (рис. 18), их равнодействующая
не лежащих в одной плоскости (рис. 18), их равнодействующая 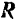 изображается по модулю и направлению диагональю параллелепипеда, построенного на векторах составляющих сил (правило параллелепипеда).
изображается по модулю и направлению диагональю параллелепипеда, построенного на векторах составляющих сил (правило параллелепипеда).
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:
| Основные определения и аксиомы статики |
| Связи и реакции связей |
| Разложение силы на сходящиеся составляющие + пример решения |
| Теорема о равновесии плоской системы трех непараллельных сил |

