Геометрический смысл модуля якобиана в двумерном случае

Оглавление:

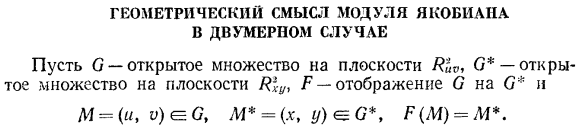
Геометрический смысл модуля якобиана в двумерном случае

Геометрический смысл модуля якобиана в двумерном случае. Пусть O-открытое множество на плоскости O*, открытое множество на плоскости B1Y, а P-отображение на C *на O. М = {U, о) 6С, м * =(х, г) ЕС *, Р(М)= М *. 46.1.Геометрический смысл модуля Якобиана Сто шестьдесят девять Карта задается парой функций х = х(u, v), то г = г(У, у). (46.1） Предположим, что P удовлетворяет следующим условиям: 1) отображение 0 на O *в полном блоке. 2) o непрерывно дифференцируемо. 3) Якобиан d {u, n) = ^ ^не исчезает в C. Обратите внимание, что на карте Р − 1, которая является инверсией Р, тоже непрерывно дифференцируемых 1-в-1 карта, где Якобиан не равен нулю в o *(см.§ 41.7).Поэтому карта является, в частности, является дифференциально-homogram из открытого множества O на С *(см. Определение в§ 41.7, 11). если y-простой замкнутый контур с O, то из-за взаимной уникальности отображения P его изображение y * = P(y) также является простым замкнутым контуром. Лемма 1.

Это утверждение было получено как прямой результат только общности отображения G. конечно, в этом случае сразу следует из приведенных выше сильных предположений. Людмила Фирмаль

Γ-ограниченное множество, и Γο. Γ* = P (Γ) также является ограниченным открытым множеством、 ДП (Т)= Р(ДТ). (46.2） Доказательство. Поскольку P и P1 являются гомоморфными отображениями, для каждого из них открытое множество сопоставляется с открытым set. As в результате, например, внутренняя точка набора гамма или гамма*передается во внутреннюю точку изображения, а граничная точка-в граничную точку. Фактически, например, существует окрестность V = 11 (M), где M —внутренняя точка множества Γ, то есть G. G и II. тогда окрестность точки M * = P II * P(II) (M) находится в G*. Второй * С. Γ*, что М *является внутренней точкой множества Γ**. Где M-граничная точка множества Γ, M * = P (M), А II * точка окрестности точки M*.

Поскольку отображение Р находится в фазе, множество V = P1 (P *) является окрестностью точки M и является медовым, поэтому окрестность I /имеет как точки, принадлежащие множеству, так и точки, которые не принадлежат. Поэтому некоторые точки принадлежат множеству Γ *, а не окрестности f *(так как эта окрестность является изображением окрестности m под отображением P, 11 = 11 (M)).То есть граничная точка фактически сопоставляется с границей. П(ДГ) С. ДГ *. (46.3） * ’ (см. результаты теоремы 41.8 в§ 7). § 46. подстановка переменных для интегралов Крата 170. Вы можете заменить символ включения знаком равенства в выражении (46.3), поскольку подобный вывод также допустим для обратного отображения.

То есть условие (46.2) является met. In кроме того, из-за открытости множества Γ также следует открытость множества Γ. Кроме того, поскольку Γ-ограниченное множество, замкнутое множество Γ также является bounded. So, согласно Лемме 41.4§ 3, множество P (T) ограничено. Поскольку P (Γ) c, ограниченный в множестве P (Γ), также означает ограниченный в множестве Γ = / Γ(Γ). П(Г). Ноль Результат: если в предположении леммы 1 граница Γ состоит из кусочно-непрерывной дифференцируемой кривой с конечным числом, то опенсеты Γ и V *имеют 2-й порядок. Доказательство. если y-непрерывная дифференцируемая кривая в множестве O, где u = u ( / ), V = V (() и^^^ b-ее представление, то функции u (1)и b(1) являются непрерывными дифференцируемыми интервалами[a, b].

При отображении P кривая y переходит в кривую y * = P( y) со следующим выражением: х (()= х(у ({), н(0), гг)= г {у (), н(0）、 Благодаря дифференциальной формуле комплексных функций (см.§ 20.3) и теореме непрерывности синтеза непрерывных функций (см.§ 19.4), функции x (1) и y {1) также имеют непрерывные производные в интервале[a, b]. 。В результате кривая y *также непрерывно дифференцируема. Это, очевидно, означает, что если y-кусочно-непрерывная дифференцируемая кривая, то есть объединение конечного числа непрерывных дифференцируемых кривых (см.§ 16.3), то y *также является кусочно-непрерывной дифференцируемой кривой. Здесь граница открытого множества dtyc.

Поскольку состоит состоит из конечной кусочно-непрерывной дифференцируемой кривой, граница г * также состоит из кусочно-непрерывной дифференцируемой кривой с конечной мерой. Людмила Фирмаль

So и dG, и EG фиксируемы (см. теорему 1 в разделе 16.5) и в результате измеренное значение равно нулю(см. теорему 4 В разделе 44.2). таким образом, в рассматриваемом случае открытое множество Γ и Γс границами меры 0 имеет 2-й порядок. Ноль (ц0.!) 0) числа e0 и некоторое. Рассмотрим замкнутый квадрат 5 (Рис. 181), где точка имеет вершину (0 0, 0°), (оо+ оо), (Л2 + а, ОО + л), (0 0, начиная с версии v0+^). (46.4） Скажем, 8 и 0(если H достаточно мал, это включение всегда будет иметь место; почему? Граница квадрата 5, состоящая из четырех сторон (d8), явно представляет собой простой замкнутый кусочно-гладкий контур. Лемма 2 результатов по набору 46.1.Геометрический смысл модуля Якобиана Сто семьдесят один $ * = P (5) (см. Рисунок 181) является замкнутым квадратом.

Обобщение на n-мерный случай.	Замена переменных в кратном интеграле.
Обобщенное интегральное неравенство Минковского.	Криволинейные координаты.