Оглавление:
Геометрический смысл модуля и аргумента производной. Понятие о конформном отображении
Пусть функция 
аналитична в точке 
и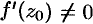 
. Выясним геометрический смысл аргумента и модуля производной.
Функция отображает точку плоскости 
в точку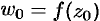 
плоскости 
.
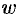Пусть произвольная точка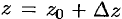 
из окрестности точки перемещается к точке по некоторой непрерывной кривой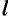 
. Тогда в плоскости 
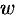соответствующая точка 
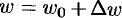будет перемещаться к точке 
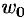по некоторой кривой 
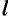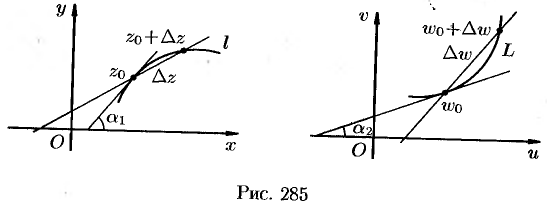
, являющейся отображением кривой в плоскости 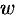(рис. 285).
По определению производной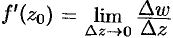 
. Отсюда следует, что 
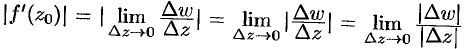. Величина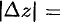 
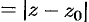представляет собой расстояние между точками и 
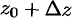, а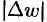 
— расстояние между точкам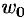и и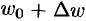 
. Следовательно, 
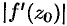есть предел отношения бесконечно малого расстояния между отображенными точкам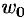и и 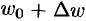к бесконечно малому расстоянию между точками и 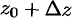. Этот предел не зависит (
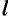аналитична в точке ) от выбора кривой , проходящей через точку . Следовательно, предел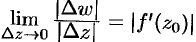 
в точке постоянен, т. е. одинаков во всех направлениях.
Отсюда вытекает геометрический смысл модуля производной: величина 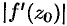определяет коэффициент растяжения (подобия) в точке при отображении . Величину 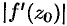называют коэффициентом растяжения, если 
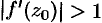, или коэффициентом сжатия, если 
.
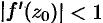Пример №74.5.
Найти коэффициент растяжения (сжатия) для функции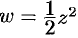 
в точке 
.
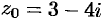Решение:
Функция 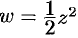аналитична в точке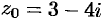, при этом 
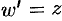. Следовательно, 
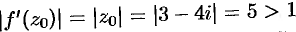. Коэффициент растяжения для функции 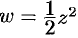в точке равен 5 (плоскость растягивается).
Для аргумента производной в точке имеем:
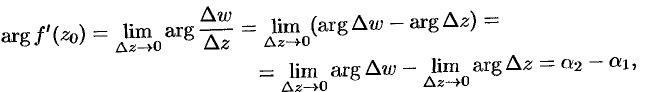
где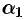 
и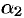 
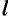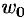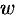— углы, которые образуют касательные к кривым и соответственно в точках , и с положительными направлениями действительных осей на плоскостях и (см. рис. 285).
Отсюда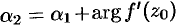 
. Это означает, что 
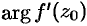— это угол, на который нужно повернуть касательную к кривой 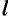в точке для того, чтобы получить направление касательной к кривой в точке 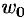. Другими словами, 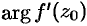— это угол между отображенным и первоначальным направлениями касательных к кривым 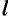и в точках и 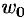соответственно. В этом состоит геометрический смысл аргумента производной .
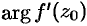В силу аналитичности функции в точке (мы предположили, что 
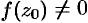) угол 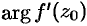один и тот же для всех кривых, проходящих через точку . Для другой пары кривых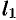 
и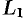 
в тех же точках и 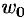будем иметь 
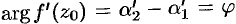. Таким образом, 
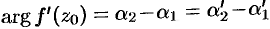, т.е. если кривые 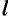и 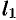образуют в точке на плоскости угол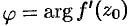 
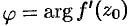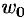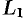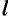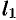, то такой же угол будут образовывать в точке кривые и , являющиеся отображениями кривых и на плоскости 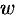(см. рис. 286).
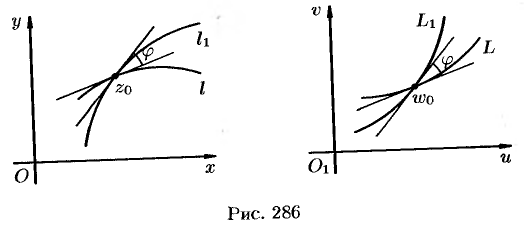
Это свойство отображения называется свойством сохранения (консерватизма) углов в точке .
Отображение , обладающее свойством сохранения углов и постоянством растяжений в точке , называется конформным (т. е. отображением, сохраняющим форму). Если при этом сохраняется и направление отсчета углов, то такое отображение называется конформным отображением 1-го рода, если направление отсчета углов изменяется на противоположное — конформным отображением 2-го рода.
Таким образом, если функция является аналитической в некоторой точке комплексной плоскости и в этой точке ее производная отлична от нуля, то отображение конформно в этой точке.
Отображение называется конформным в области 
, если оно конформно в каждой точке этой области.
Справедливо следующее утверждение: если функция аналитична в области , причем во всех точках области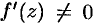 
, то отображение конформно в ; если отображение конформно в области , то функция аналитична в и во всех точках этой области .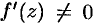
Пример №74.6.
Выяснить геометрическую картину отображения, осуществляемого функцией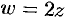 
.
Решение:
Отображение 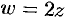конформно во всех точках плоскости , т. к.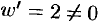 
.
Коэффициент растяжения в любой точке плоскости равен 2. Так как 
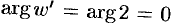, то направление при отображении не меняется. Таким образом, отображение 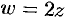есть преобразование гомотетии с центром в нулевой точке (
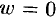при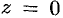 
) и коэффициентом гомотетии, равным 2.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Дифференцирование функции комплексного переменного |
| Аналитическая функция тфкп |
| Интегрирование функции комплексного переменного |
| Интегральная теорема Коши |
