Рассмотрим в качестве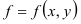 
в формуле 
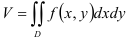единичную функцию 
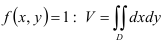. Тогда цилиндрическое тело «превратится» в прямой цилиндр с высотой, равной 1, и основанием — 
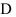. Объём такого цилиндра 
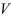численно совпадает с площадью 
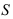его основания 
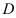. Таким образом, площадь плоской фигуры 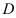можно находить по формуле:
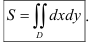
Геометрический смысл двойного интеграла от единичной функции заключается в том, что величина двойного интеграла от единичной функции но области 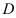равна площади плоской фигуры, представляющей собой область интегрирования .
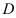Рассмотрим пример вычисления площади плоской фигуры с помощью двойного интеграла.
Пример решения заказа контрольной работы №89.2
Найдите площадь плоской фигуры, ограниченной линиями
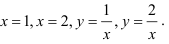
Решение:
Поскольку геометрически двойной интеграл от единичной функции по области 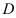равен площади плоской фигуры, представляющей собой область интегрирования 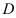, будем использовать формулу:
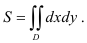
В нашем случае областью интегрирования 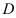является фигура, ограниченная линиями
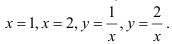
Вычислим
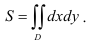
Для этого построим область интегрирования 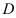в прямоугольной декартовой системе координат на плоскости.
Линии, задаваемые уравнениями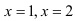 
— прямые, параллельные оси 
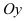и проходящие соответственно через точки (1;0), (2;0). Линия, задаваемая уравнением 
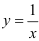— гипербола, «ветви» которой расположены в I и III координатных четвертях. Гиперболу 
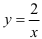можно получить из гиперболы 
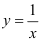с помощью растяжения последней вдоль оси ординат в два раза.
Описание линий, задающих область интегрирования 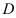, позволяет при ее построении ограничиться I координатной четвертью.
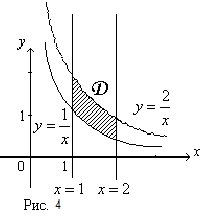
Изображенная на рисунке область интегрирования 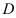(рис.4) является криволинейной областью. Поэтому для вычисления двойного интеграла используем соответствующую формулу сведения его к повторному интегралу:
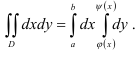
В нашем случае
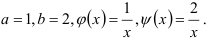
Следовательно,
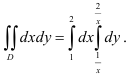
Вычислим полученный повторный интеграл:
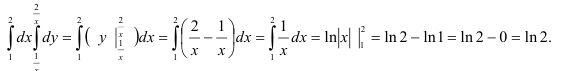
В итоге,
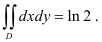
Следовательно,
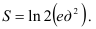
Ответ:
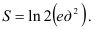
На этой странице вы сможете заказать контрольную работу и познакомиться с теорией и другими примерами решения:
Заказать контрольную работу по высшей математике
Другие похожие примеры возможно вам будут полезны:
| Признак Даламбера для общего члена ряда |
| Основные свойства рядов |
| Пример вычисления подобного повторного интеграла |
| Нахождение дифференциала второго порядка функции |
