В силу геометрического смысла двойного интеграла от неотрицательной функции, для вычисления объема цилиндрического тела используется формула:
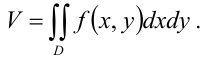
В качестве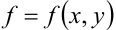 
в данной формуле рассмотрим единичную функцию 
: 
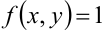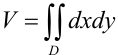. Тогда цилиндрическое тело «превратится» в прямой цилиндр с высотой, равной 1, и основанием — 
. Как известно, объем такого цилиндра 
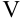численно совпадает с площадью 
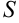его основания или, что то же самое, площадь плоской фигуры можно находить по формуле:
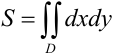
Следовательно, величина двойного интеграла от единичной функции по области равна площади плоской фигуры, представляющей собой область интегрирования . В этом и заключается геометрический смысл двойного интеграла от единичной функции.
Получено основание для широкого использования двойного интеграла в целях вычисления площади плоской фигуры. Следует заметить, что по сравнению с уже известной техникой определенного интегрирования для вычисления площадей плоских фигур техника двойного интегрирования является более общей и, как правило, более удобной.
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
