Оглавление:
Геометрический смысл дифференциала
Дифференциал функции равен приращению ординаты касательной к графику данной функции, когда аргумент получает приращение 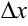 .
.
Задача №54.
Дана функция 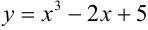 . Найти выражение для дифференциала.
. Найти выражение для дифференциала.
Решение:
По формуле 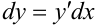 получаем
получаем
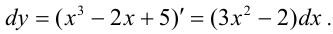
Из определения дифференциала выводится формула
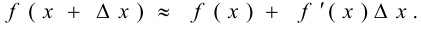
Эта формула позволяет вычислить приближённое значение функции, соответствующее приращённому значению аргумента, если известно её значение в некоторой точке и значение производной в этой точке, когда приращение аргумента является достаточно малым. Например, для функции 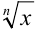 имеем
имеем
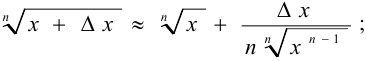
для 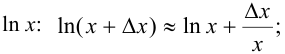
для 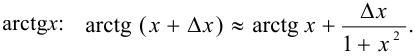
Задача №55.
Вычислить приближённое значение 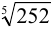 , если
, если 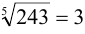 .
.
Решение:
Имеем 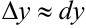 , т. е.
, т. е. 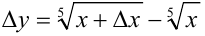 .
.
В нашем примере 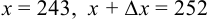 , тогда
, тогда 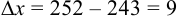 .
.
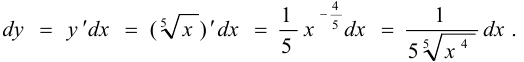
Отсюда
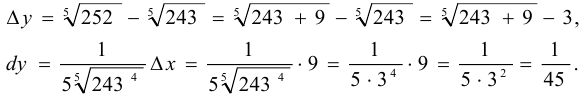
Поэтому
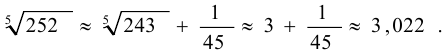
Иначе по формуле 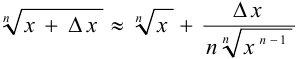
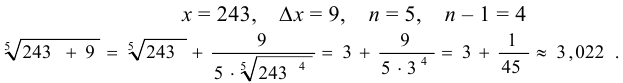
Задача №56.
Вычислить 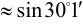 , зная, что
, зная, что 
Решение:
Воспользуемся формулой
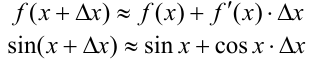
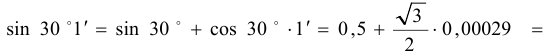
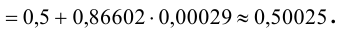
Задача №57.
Вычислить натуральный логарифм числа 2,001 с пятью знаками после запятой 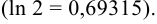
Решение:
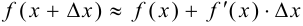
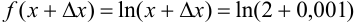 , где
, где 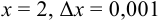 .
.
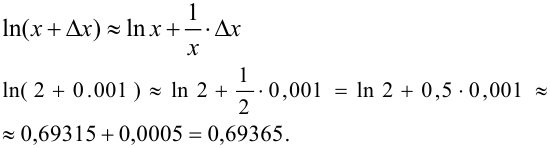
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:

