Геометрический смысл частных производных функции двух переменных
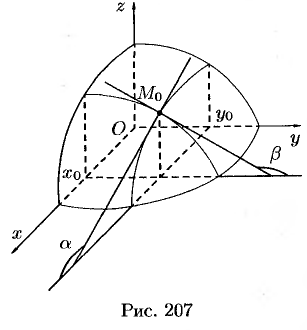
Графиком функции 
является некоторая поверхность (см. п. 12.1). График функции 
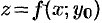есть линия пересечения этой поверхности с плоскостью 
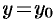. Исходя из геометрического смысла производной для функции одной переменной (см. п. 20.2), заключаем, что 
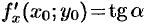, где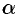 
— угол между осью 
и касательной, проведенной к кривой 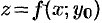в точке 
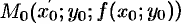(см. рис. 207).
Аналогично,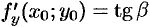 
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Свойства функций, непрерывных в ограниченной замкнутой области |
| Частные производные первого порядка |
| Частные производные высших порядков |
| Дифференцируемость и полный дифференциал функции |
