Геометрически функция двух действительных переменных 
представляет собой поверхность в пространстве, в котором введена прямоугольная система координат 
.
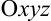Обозначим буквой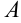 
некоторую точку рассматриваемой поверхности с координатами 
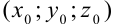, где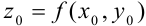 
.
Проведем через точку 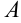плоскость, параллельную оси 
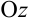и перпендикулярную оси 
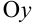, уравнение которой имеет вид 
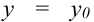. При пересечении плоскости и данной поверхности получим кривую, проходящую через точку 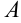и принадлежащую поверхности. Эта кривая в плоскости 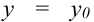(рис. 26.1) имеет уравнение 
.
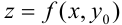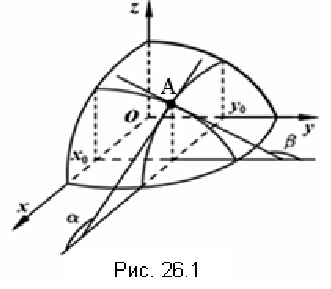
Исходя из геометрического смысла производной функции одной переменной, заключаем, что частная производная функции по переменой 
в точке 
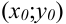дает угловой коэффициент (тангенс угла наклона) касательной к линии 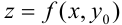пересечения поверхности с плоскостью, параллельной координатной плоскости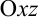 
, в точке .
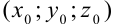Таким образом, частная производная функция по переменной в точке 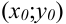дает возможность оценить «крутизну» поверхности в точке 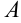, или скорость изменения функции по направлению, параллельному оси 
.
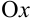Вопрос о геометрическом смысле частной производной функции по переменной 
в точке 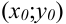решается аналогичным образом. Так,
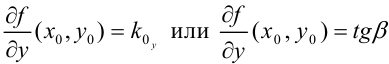
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
