Геометрический подход
Иногда задачи могут быть решены с помощью геометрического подхода. Рассмотрим один из таких примеров.
Пример №395.
Решить уравнение
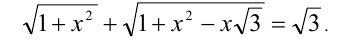
Решение:
Придадим каждому из двух радикалов в уравнении определённый геометрический смысл. Действительно, рассмотрим прямоугольный треугольник 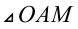 со сторонами
со сторонами 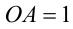 ,
, 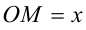 и углом
и углом 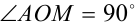 между ними. Тогда геометрический смысл первого из радикалов
между ними. Тогда геометрический смысл первого из радикалов 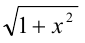 есть длинна гипотенузы
есть длинна гипотенузы 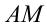 .
.
Рассмотрим теперь треугольник 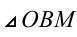 со сторонами
со сторонами 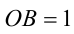 ,
, 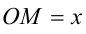 и углом
и углом 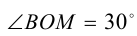 между ними. Тогда геометрический смысл второго корня
между ними. Тогда геометрический смысл второго корня
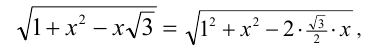
согласно теореме косинусов, есть длина третьей стороны 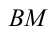 этого треугольника.
этого треугольника.
Изобразим оба треугольника с общей стороной на одном рисунке и соединим отрезком точки
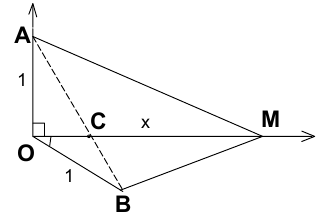
на одном рисунке и соединим отрезком точки  и
и 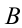 . Согласно неравенству треугольника, имеем:
. Согласно неравенству треугольника, имеем: 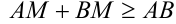 , причем
, причем 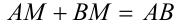 тогда и только тогда, когда точка
тогда и только тогда, когда точка 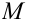 лежит между точками
лежит между точками 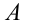 и
и 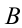 , совпадая с
, совпадая с 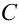 .
.
Введём систему координат, поместив начало координат в точку 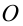 и направив ось абсцисс вдоль стороны
и направив ось абсцисс вдоль стороны 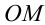 , а ось ординат — перпендикулярно ей вдоль стороны
, а ось ординат — перпендикулярно ей вдоль стороны 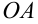 . Тогда в выбранной системе координат
. Тогда в выбранной системе координат 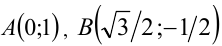 , и длина отрезка
, и длина отрезка 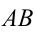 равна
равна
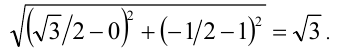
Так как в правой части уравнения стоит как раз 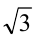 , то решить уравнение означает найти абсциссу точки
, то решить уравнение означает найти абсциссу точки 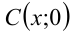 , в которой прямая
, в которой прямая 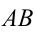 пересекает ось абсцисс. Уравнение прямой
пересекает ось абсцисс. Уравнение прямой  имеет вид
имеет вид 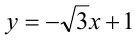 . Составляя уравнение
. Составляя уравнение 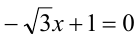 , находим искомое и единственное решение
, находим искомое и единственное решение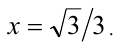
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:
Эти страницы возможно вам будут полезны:

