Оглавление:



Геометрический и физической смысл определенного интеграла
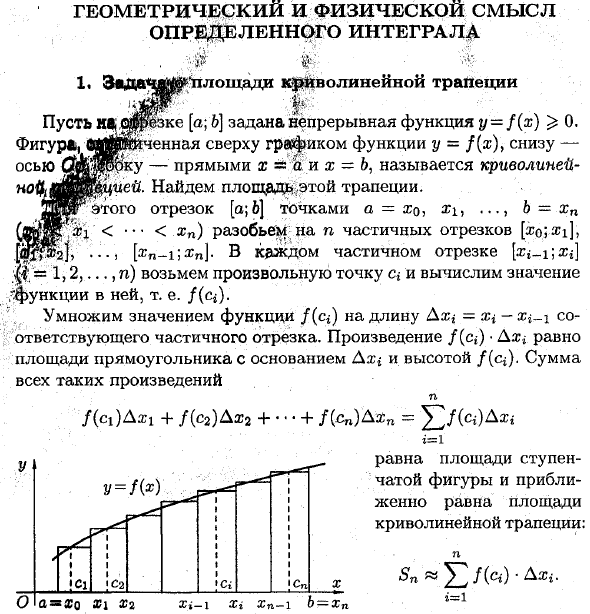
- Упрощенный интегральный геометрический и физический смысл , , ; • # Щ ■ Щ 1. Эвда ^ чшы ^ ‘квадратная кривая трапеции Привет, С ^^ ке [а, b] диаграмма непрерывная функция YF (х) ^ 0 задается *, графически показаны на функции у = F (X) на оси -UWFrK снизу — прямой а сс (I и x = называются криволинейными шиями. Найдите эту трапециевидную область.
. / (Ci). Умножьте значение функции f (c *) на соответствующую частичную длину сегмента J, = X {-Xi — 1. Произведение / (s,) Axi равно площади прямоугольника с основанием Axi и высотой / (s ^).
Разделите отрезок [a \ b] в точке a = x0, xi. Xi] = = 1,2, …, n) получить произвольную точку c в каждом частичном сегменте и вычислить значение функции в нем, т.е Людмила Фирмаль
Сумма всех таких работ 71 f (c ) Ax \ + f (c2) Ax2 + α • + + (cn) Axn = £ / (<*) Дх < я = я Эквивалентно площади фигуры лестницы и приблизительно равно площади изогнутой трапеции:
Уменьшение всех значений Axi повышает точность аппроксимации изогнутой трапеции с ступенчатыми числами и точность получаемой формулы. Следовательно, для точного значения площади S изогнутой трапеции, предела S, на который направлена область ступенчатой фигуры 5P, когда n увеличивается бесконечно и Л = максимальная ось> 0. N Это но Таким образом, конкретный интеграл неотрицательной функции численно равен площади искривленной трапеции. Это геометрический смысл конкретного интеграла.
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Рабочая проблема переменной интенсивности Переместите массу M под действием силы Fy, которая ориентирована вдоль оси Ox и имеет переменные значения от F до F (x). Где х — абсцисса движущейся точки М. Найдите работу A с силой F, перемещающую точку M из точки x = a вдоль точки x = t b (a b = xn (ao (c *) D: r * = JF (x) dx. 1 = 1
Следовательно, действие переменной силы F заключается в том, что значение представляет собой непрерывную функцию F = F (x), а сегмент [a; 6] представляет собой конкретный интеграл от величины силы F (x) в интервале [a; равны. Б]. Это физический смысл конкретного интеграла. Аналогично, путь 5, пройденный одной точкой за период от t = a до t = 6, показан равным некоторому интегралу скорости b. S = Jv (t) dt \ но Масса t [a; B] неоднородного стержня на отрезке явно равна , В;.
Интеграл плотности y (x): m = J7 (x) .dx. ■ Людмила Фирмаль

