Оглавление:


Геометрические условия равновесия плоской системы сходящихся сил
- Система сил, в которой геометрические условные линии действия равновесного состояния плоской системы сходящихся сил пересекаются в одной точке, называется системой сходящихся сил.
В предыдущем пункте уже указывалось, что любая система сходящихся сил может быть заменена результатом, равным основному вектору данной силовой системы, если система сходящихся сил находится в равновесии,
в результате чего, соответственно, ее основной вектор равен нулю. Людмила Фирмаль
Согласно двум методам определения основного вектора, равновесное состояние системы сходящейся силы также может быть записано в двух формах. Рассмотрим сначала геометрические условия равновесия системы сходящихся сил. Теорема гласит, что для равновесия свободных тел под действием плоской системы
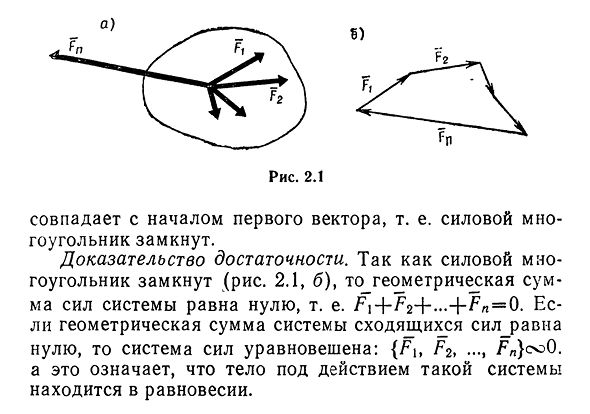
сходящихся сил необходимо и достаточно, чтобы силовые полигоны, построенные из этих сил, были замкнуты. Доказательство необходимости. Под действием системы сходящихся сил задается твердое тело в равновесии{?I, F2,_…,?P} (рис. 2.1, а). Следовательно, в
- соответствии с§1.1, {?I, F2 * * * * » FN}coO. Другой-сто-роны и, согласно 4-й аксиоме, {Fj, Fn}co сохраняют, следовательно, Gravnsoo. Результирующая гравитация является конечным вектором силового многоугольника и равна нулю, поэтому она является концом
последнего вектора В начале первого вектора и 20совпадает, то есть силовой полигон замыкается. Доказательство адекватности. Поскольку силовой полигон замкнут(рис. 2.1, б), геометрическая сумма сил системы равна нулю, то есть F i+F2+…+F n=0.
Если геометрическая сумма системы сходящихся сил равна нулю, то Людмила Фирмаль
система сил уравновешивается: {Fh F2,••*, F n}coO. Это означает, что организм под действием такой системы находится в равновесии.
Смотрите также:
| Виды связей и их реакции | Нормальные напряжения при косом изгибе |
| Основные понятия векторной алгебры | Касательные напряжения при изгибе балки |

