Оглавление:
Оптика — раздел физики, в котором изучается излучение света, его распространение и взаимодействие с веществом.
Различают геометрическую, волновую и квантовую оптику. В геометрической оптике не учитывается природа света, а его распространение в пространстве рассматривается, исходя из представлений о световых лучах. Световой луч — это линия, вдоль которой распространяется световая энергия.
формулы геометрической оптики
Закон отражения
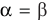
Здесь 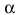 — угол падения (рад),
— угол падения (рад), 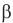 — угол отражения (рад).
— угол отражения (рад).
Закон преломления

Здесь 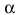 — угол падения (рад),
— угол падения (рад), 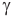 — угол преломления (рад),
— угол преломления (рад), 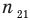 — показатель преломления второй среды относительно первой (безразмерный),
— показатель преломления второй среды относительно первой (безразмерный), 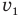 — скорость света в первой среде (м/с),
— скорость света в первой среде (м/с), 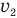 — скорость света во второй среде (м/с).
— скорость света во второй среде (м/с).
Физический смысл абсолютного показателя преломления
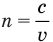
Здесь n — абсолютный показатель преломления (безразмерный), с — скорость света в вакууме (м/с), и — скорость света в прозрачной среде (м/с).
Физический смысл относительного показателя преломления
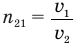
Здесь 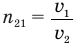
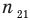 — показатель преломления второй среды относительно первой,
— показатель преломления второй среды относительно первой, 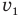 — скорость света в первой среде (м/с),
— скорость света в первой среде (м/с), 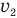 — скорость света во второй среде.
— скорость света во второй среде.
Связь относительного показателя преломления двух сред с их абсолютными показателями преломления
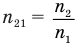
Здесь 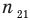 — относительный показатель преломления сред (безразмерный),
— относительный показатель преломления сред (безразмерный), 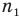 — абсолютный показатель преломления первой среды,
— абсолютный показатель преломления первой среды, 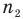 — абсолютный показатель преломления второй среды.
— абсолютный показатель преломления второй среды.
Формула предельного угла полного отражения
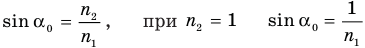
Здесь 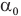 — предельный угол полного отражения (рад),
— предельный угол полного отражения (рад), 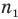 — абсолютный показатель преломления первой среды (безразмерный),
— абсолютный показатель преломления первой среды (безразмерный), 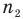 — абсолютный показатель преломления второй среды (безразмерный).
— абсолютный показатель преломления второй среды (безразмерный).
Формула линзы

Здесь d — расстояние от предмета до линзы (м), f — расстояние от линзы до изображения (м), F — фокусное расстояние линзы (м), D — оптическая сила линзы (дптр).
Формула оптической силы линзы
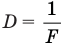
Все величины названы в предыдущей формуле
Линейное увеличение линзы

Здесь Г — линейное увеличение линзы (безразмерное), Н — линейный размер изображения (м), h — линейный размер предмета (м), d — расстояние от предмета до линзы (м), f — расстояние от линзы до изображения (м).
Линейное увеличение лупы
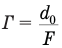
Здесь 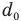 = 25 см — расстояние наилучшего зрения, F — фокусное расстояние лупы.
= 25 см — расстояние наилучшего зрения, F — фокусное расстояние лупы.
Свет в однородной и изотропной среде распространяется прямолинейно. Доказательством этому служит образование тени и полутени. Если источник света S точечный, то позади непрозрачного предмета М образуется тень (рис. 324, а),
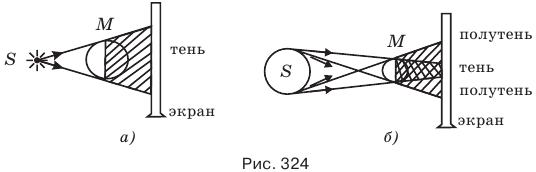
а если источник света S протяженный, то позади предмета ^образуются тень и полутени (рис. 324, б).
Точечным источником света называют абстрактный источник, представляющий собой светящуюся материальную точку. Если точечный источник света удален в бесконечность, то его лучи падают на освещаемый предмет параллельным пучком.
Световой луч не может быть бесконечно тонким. При прохождении сквозь отверстие, в котором умещается несколько длин волн, он расширяется вследствие дифракции и загибает в область геометрической тени.
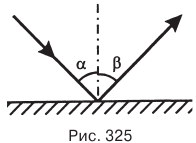
При падении световых лучей на непрозрачную гладкую преграду они меняют направление, возвращаясь в прежнюю среду. Это явление называется отражением света. Угол между падающим лучом и перпендикуляром к отражающей свет поверхности называется углом падения а. Угол между отраженным лучом и перпендикуляром к отражающей поверхности называется углом отражения 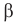 (рис. 325).
(рис. 325).
Законы отражения
Законы отражения:
- луч падающий и луч отраженный всегда лежат в одной плоскости с перпендикуляром, проведенным в точку падения к отражающей поверхности, по разные стороны от него;
- угол отражения всегда равен углу падения,
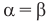 .
.
Если луч падает перпендикулярно отражающей поверхности, то угол падения равен нулю, поэтому и угол отражения тоже равен нулю. В этом случае луч отражается в обратном направлении — сам по себе.
На законе отражения основано получение изображения в плоском зеркале.
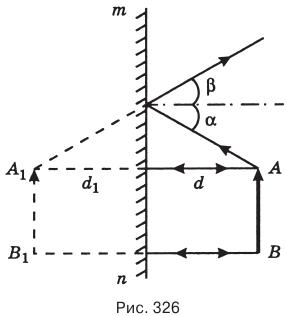
Плоское зеркало mn дает мнимое и прямое изображение 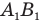 равное по размеру предмету АВ и расположенное от зеркала на таком же расстоянии, что и предмет (рис. 326). Исключение составляет случай, когда на плоское зеркало падает пучок сходящихся лучей (рис. 327) — в этом случае изображение S получится действительным.
равное по размеру предмету АВ и расположенное от зеркала на таком же расстоянии, что и предмет (рис. 326). Исключение составляет случай, когда на плоское зеркало падает пучок сходящихся лучей (рис. 327) — в этом случае изображение S получится действительным.
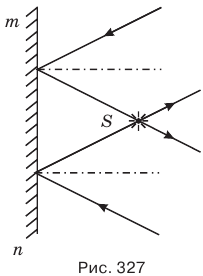
Если поверхности двух плоских зеркал образуют угол 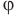 (рис. 328), количество изображений N в такой системе зеркал можно определить по формуле
(рис. 328), количество изображений N в такой системе зеркал можно определить по формуле
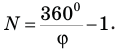
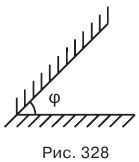
При переходе света из одной прозрачной среды в другую меняется направление светового луча. Это явление называется преломлением света. Угол между преломленным лучом и перпендикуляром к преломляющей поверхности называется углом преломления (рис. 329).
Законы преломления
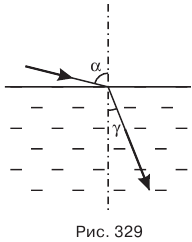
Законы преломления:
- луч падающий и луч преломленный всегда лежат в одной плоскости с перпендикуляром, опущенным в точку падения луча к преломляющей поверхности, по разные стороны от перпендикуляра;
- отношение синуса угла падения
к синусу угла преломления есть величина постоянная для данных двух сред и называется показателем преломления второй среды относительно первой 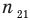 :
:
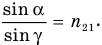
При этом первой средой является та среда, в которой распространяется падающий луч, а второй средой — та, в которой распространяется преломленный луч. Например, если свет переходит из воды в стекло, то 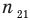 — это показатель преломления стекла относительно воды, а если наоборот, из стекла в воду, то
— это показатель преломления стекла относительно воды, а если наоборот, из стекла в воду, то 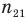 — показатель преломления воды относительно стекла.
— показатель преломления воды относительно стекла.
Если луч переходит из вакуума (воздуха) в прозрачную среду, то показатель преломления этой среды относительно вакуума называется абсолютным показателем преломления этой среды п. Значение абсолютного показателя преломления каждой среды приводится в справочных данных.
Абсолютный показатель преломления среды показывает, во сколько раз скорость света в вакууме больше, чем в данной среде:
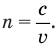
Относительный показатель преломления 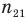 равен отношению абсолютного показателя преломления второй среды к относительному показателю преломления первой среды:
равен отношению абсолютного показателя преломления второй среды к относительному показателю преломления первой среды:
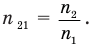
Физический смысл относительного показателя преломления: относительный показатель преломления показывает, во сколько раз отличается скорость света в первой среде от скорости света во второй среде: 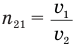 .
.
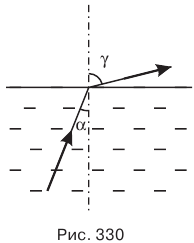
Та среда, у которой абсолютный показатель преломления больше, называется оптически более плотной. Если свет переходит из оптически более плотной среды в оптически менее плотную, например, из воздуха в воду, то угол падения больше угла преломления. И наоборот, если луч переходит из оптически более плотной среды в оптически менее плотную, например, из воды в воздух, то угол падения меньше угла преломления (рис. 330).
В случае перехода луча из оптически более плотной среды в оптически менее плотную существует такой угол падения 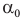 , при котором преломленный луч скользит по границе раздела сред с разной оптической плотностью. При этом угол преломления равен 90°. Такой угол падения называется предельным углом полного отражения (рис. 331).
, при котором преломленный луч скользит по границе раздела сред с разной оптической плотностью. При этом угол преломления равен 90°. Такой угол падения называется предельным углом полного отражения (рис. 331).
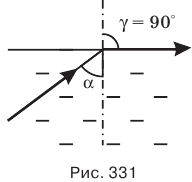
Если луч упадет на поверхность под углом больше предельного, то он полностью отразится обратно в первую среду (рис. 332). Такое явление называется полным отражением.
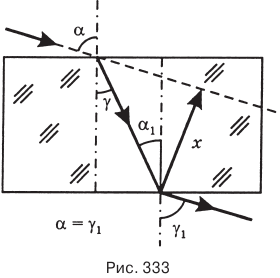
Проходя сквозь
плоскопараллельную пластинку из вещества, оптически более плотного, чем окружающая среда, луч не меняет своего направления, а лишь смещается на расстояние х (рис. 333). Смещение луча х тем больше, чем толще пластинка и чем больше показатель преломления ее вещества.
Проходя сквозь треугольную призму, изготовленную из оптически более плотного, чем окружающая среда, вещества, луч дважды преломляется, отклоняясь к ее основанию (рис. 334). При этом изображение 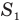 источника света S смещается к вершине призмы. Угол
источника света S смещается к вершине призмы. Угол 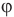 , лежащий против основания призмы, называется преломляющим углом призмы. Угол
, лежащий против основания призмы, называется преломляющим углом призмы. Угол 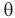 между направлениями упавшего на призму и вышедшего из
между направлениями упавшего на призму и вышедшего из
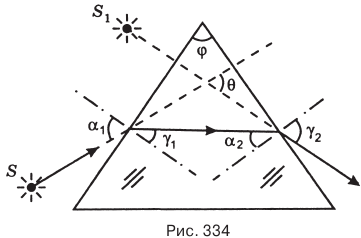
призмы лучей называется углом отклонения луча. Угол отклонения 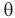 зависит от угла падения луча на призму
зависит от угла падения луча на призму 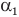 , преломляющего угла призмы
, преломляющего угла призмы 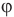 и показателя преломления n вещества, из которого она изготовлена.
и показателя преломления n вещества, из которого она изготовлена.
Линзой называют прозрачное для света тело, ограниченное сферическими или иными криволинейными поверхностями, одна из которых может быть плоской. Если линза в средней части толще, чем у краев, то она называется выпуклой, а если наоборот, — то вогнутой.
Двояковыпуклая линза называется собирающей, т.к. она собирает после преломления параллельные лучи в одной точке (рис. 335, а).
Вершины сферических сегментов 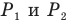 , образующих линзу, называются ее полюсами. Точка, в которой сливаются полюсы бесконечно тонкой линзы, называется ее главным оптическим центром О.
, образующих линзу, называются ее полюсами. Точка, в которой сливаются полюсы бесконечно тонкой линзы, называется ее главным оптическим центром О.
Прямая mn, проходящая через центры сфер 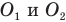 , поверхности которых образуют линзу, называется главной оптической осью линзы. Точка, в которой пересекаются лучи, падающие на линзу параллельно ее главной оптической оси, называется фокусом линзы F. Фокус линзы F делит расстояние между центром сферы
, поверхности которых образуют линзу, называется главной оптической осью линзы. Точка, в которой пересекаются лучи, падающие на линзу параллельно ее главной оптической оси, называется фокусом линзы F. Фокус линзы F делит расстояние между центром сферы 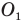 и главным оптическим центром линзы пополам, поэтому центр
и главным оптическим центром линзы пополам, поэтому центр 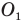 называют двойным фокусом линзы 2F.
называют двойным фокусом линзы 2F.
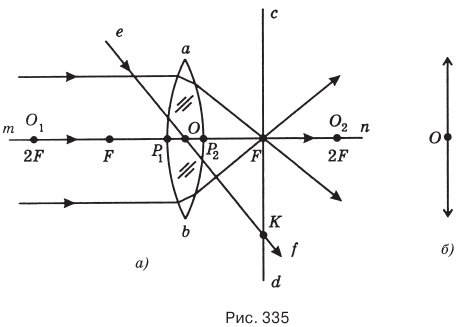
Расстояние OF от фокуса линзы до ее главного оптического центра называется фокусным расстоянием линзы и тоже обозначается буквой F. Собирающая линза имеет два действительных фокуса F и два двойных фокуса 2F, расположенных по обе стороны линзы. На рис. 335,6) показано условное изображение собирающей линзы.
Любой луч, проходящий через главный оптический центр линзы О, не преломляется. Такой луч называется побочной осью линзы.
Плоскость cd, проходящая через фокус линзы перпендикулярно ее главной оптической оси, называется фокальной плоскостью линзы.
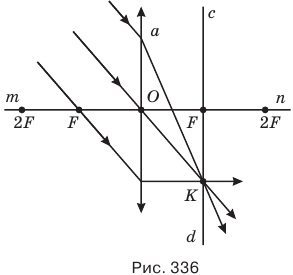
Главное свойство фокальной плоскости собирающей линзы: она является геометрическим местом точек, в которых пересекаются параллельные лучи, падающие на собирающую линзу под разными углами (рис. 336).
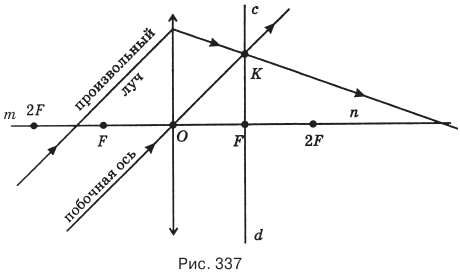
Чтобы узнать, как пойдет после преломления произвольный луч, упавший на собирающую линзу, надо провести через главный оптический центр линзы побочную ось, параллельную произвольному лучу и построить с другой стороны линзы главную фокальную плоскость cd. Побочная ось не преломится в линзе и пересечет главную фокальную плоскость cd в некоторой точке К. А поскольку побочная ось параллельна произвольному лучу, то он после преломления тоже пойдет через точку К (рис. 337).
Если на линзу падает пучок параллельных лучей, значит, их источник расположен в бесконечности, т.е. расстояние от источника до линзы 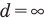 . Если такие лучи параллельны главной оптической оси, то после преломления они пересекутся в фокусе линзы F — там появится действительное изображение
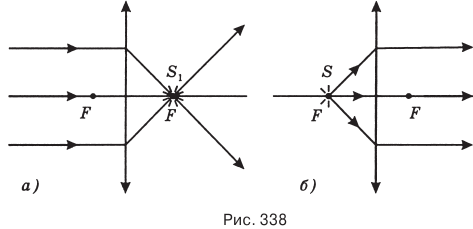
. Если такие лучи параллельны главной оптической оси, то после преломления они пересекутся в фокусе линзы F — там появится действительное изображение  источника S, удаленного в бесконечность (рис. 338, а). Световые лучи обратимы. Это значит, что если в фокус собирающей линзы поместить точечный источник света S, то после преломления в линзе его лучи пойдут параллельно главной оптической оси линзы и изображение
источника S, удаленного в бесконечность (рис. 338, а). Световые лучи обратимы. Это значит, что если в фокус собирающей линзы поместить точечный источник света S, то после преломления в линзе его лучи пойдут параллельно главной оптической оси линзы и изображение  источника уйдет в бесконечность, т.е. расстояние от линзы до изображения
источника уйдет в бесконечность, т.е. расстояние от линзы до изображения 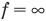 (рис. 338, б).
(рис. 338, б).
Как правило, если в условии задачи не сказано, о какой линзе идет речь, значит, это собирающая линза. Если у вас имеется хотя бы часть линзы, изображение в ней строится так же, как если бы это была целая линза.
Двояковогнутая линза рассеивает пучки параллельных лучей, падающих на нее, поэтому она называется рассеивающей линзой. Если пучок лучей падает на рассеивающую линзу параллельно ее главной оптической оси, то после преломления в линзе их мнимые продолжения пересекаются в одной точке,
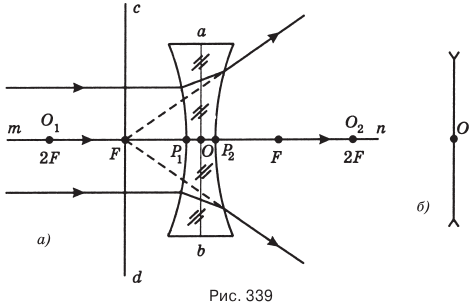
которая является мнимым фокусом F рассеивающей линзы (рис. 339, а). Рассеивающая линза имеет два мнимых фокуса F, расположенных на главной оптической оси по обе стороны от нее на середине отрезка 0,0. На рис. 339, б) показано условное изображение рассеивающей линзы.
Плоскость cd, перпендикулярная главной оптической оси и проходящая через фокус рассеивающей линзы, называется главной фокальной плоскостью этой линзы.
Главное свойство фокальной плоскости рассеивающей линзы: она является геометрическим местом точек, в которых пересекаются мнимые продолжения любых параллельных лучей, падающих на линзу под разными углами (рис. 340).
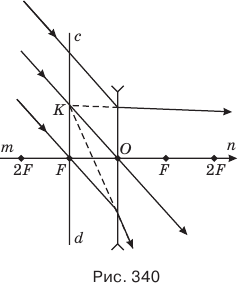
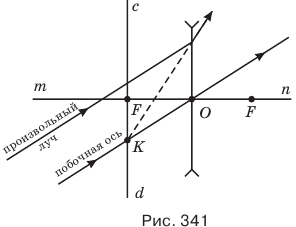
Чтобы узнать, как пойдет упавший на рассеивающую линзу произвольный луч после преломления, надо провести параллельную ему побочную ось и построить главную фокальную плоскость cd с той же стороны линзы, где лежит и произвольный луч. Точку К, в которой побочная ось пересечет главную фокальную плоскость, надо соединить с точкой падения произвольного луча на линзу его мнимым (штриховым) продолжением, а сам луч пойдет в противоположном направлении (рис. 341).
Мнимые лучи и мнимые изображения предметов принято изображать штриховыми линиями.
Чтобы построить изображение светящейся точки в линзе, надо знать, где пересекутся после преломления испущенные этой точкой два любых луча. Лучше выбрать лучи, про которые вы знаете, как они пойдут после преломления.
Чтобы построить изображение предмета АВ, надо сначала построить изображение точки А, не лежащей на главной оптической оси. Для этого сначала из точки А проведем к линзе луч, параллельный главной оптической оси, — после преломления он пойдет через фокус. Затем из этой же точки А провести через главный оптический центр линзы О побочную ось. Точка 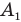 , в которой после преломления пересекутся эти два луча, и будет изображением точки А. Затем, если предмет АВ был перпендикулярен главной оптической оси mn, опустить из точки А, на главную оптическую ось перпендикуляр и в его основании на оси получить изображение
, в которой после преломления пересекутся эти два луча, и будет изображением точки А. Затем, если предмет АВ был перпендикулярен главной оптической оси mn, опустить из точки А, на главную оптическую ось перпендикуляр и в его основании на оси получить изображение 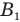 точки В.
точки В.
Если предмет АВ находится за двойным фокусом собирающей линзы, то его действительное изображение 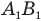 будет обратным (перевернутым), уменьшенным и расположится между фокусом F и двойным фокусом 2F по другую сторону линзы (рис. 342, а). Если предмет АВ расположен в двойном фокусе 2F, то его действительное изображение
будет обратным (перевернутым), уменьшенным и расположится между фокусом F и двойным фокусом 2F по другую сторону линзы (рис. 342, а). Если предмет АВ расположен в двойном фокусе 2F, то его действительное изображение 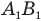 будет обратным, равным по размерам самому предмету и тоже расположенным в двойном фокусе по другую сторону линзы (рис. 342, б). Если предмет
будет обратным, равным по размерам самому предмету и тоже расположенным в двойном фокусе по другую сторону линзы (рис. 342, б). Если предмет
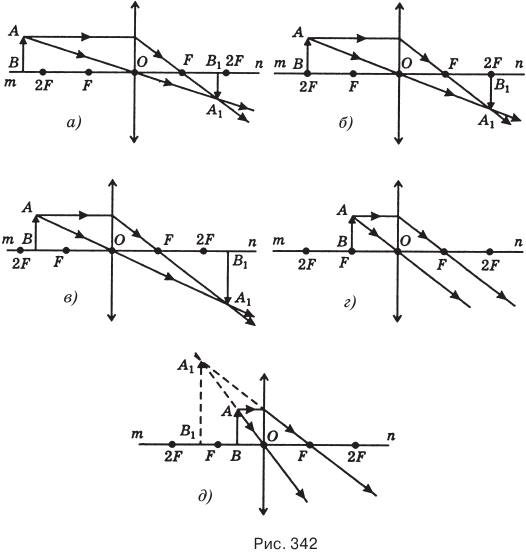
АВ находится между двойным фокусом 2F и фокусом F, то его действительное изображение 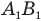 будет увеличенным, обратным и расположится за 2F по другую сторону линзы (рис. 342, в). Если предмет АВ находится в фокусе линзы F, то его изображение уйдет в бесконечность (рис. 342, г). И наконец, если предмет АВ находится между фокусом F и линзой, то его мнимое изображение
будет увеличенным, обратным и расположится за 2F по другую сторону линзы (рис. 342, в). Если предмет АВ находится в фокусе линзы F, то его изображение уйдет в бесконечность (рис. 342, г). И наконец, если предмет АВ находится между фокусом F и линзой, то его мнимое изображение 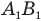 в собирающей линзе будет прямым, увеличенным и расположится с той же стороны линзы, что и сам предмет АВ (рис. 343, д).
в собирающей линзе будет прямым, увеличенным и расположится с той же стороны линзы, что и сам предмет АВ (рис. 343, д).
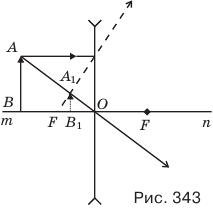
Изображение AjB, предмета АВ в рассеивающей линзе будет всегда мнимым, прямым и уменьшенным (этим оно отличается от мнимого изображения в собирающей линзе, там оно увеличенное, см. рис. 342, д) и расположенным по ту же сторону линзы, что и сам предмет (рис. 343).
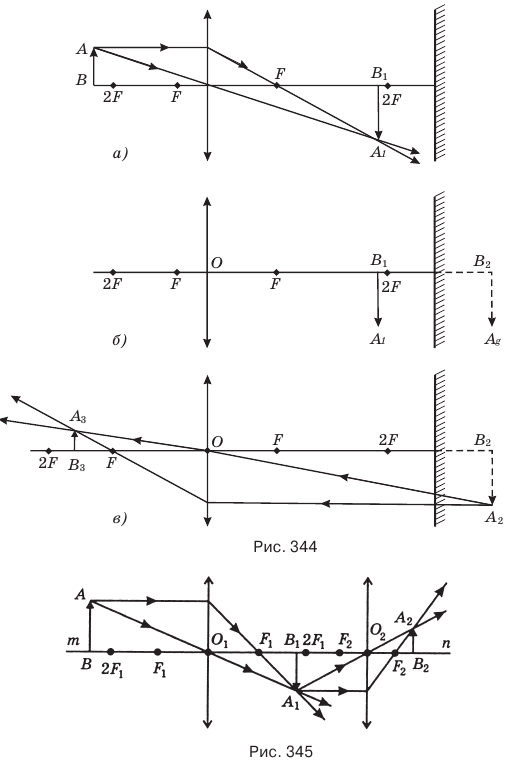
Если требуется построить изображение предмета АВ в системе собирающая линза — плоское зеркало, то сначала постройте изображение 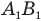 в линзе (рис. 344, а). Это изображение
в линзе (рис. 344, а). Это изображение 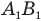 станет предметом по отношению к зеркалу. Затем постройте изображение
станет предметом по отношению к зеркалу. Затем постройте изображение 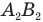 предмета
предмета 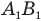 уже в плоском зеркале (рис. 344, б). Это изображение
уже в плоском зеркале (рис. 344, б). Это изображение 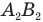 станет вторым предметом по отношению к линзе. И, наконец, постройте еще одно изображение
станет вторым предметом по отношению к линзе. И, наконец, постройте еще одно изображение 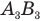 предмета
предмета 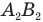 в линзе (рис. 344, в). Изображение
в линзе (рис. 344, в). Изображение 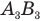 и станет окончательным изображением предмета АВ, даваемым системой линза — зеркало. Если требуется построить изображение предмета в системе двух линз, например, собирающих, то сначала постройте изображение
и станет окончательным изображением предмета АВ, даваемым системой линза — зеркало. Если требуется построить изображение предмета в системе двух линз, например, собирающих, то сначала постройте изображение 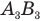 предмета АВ в первой, левой линзе (рис. 345). Это изображение
предмета АВ в первой, левой линзе (рис. 345). Это изображение 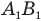 станет предметом для второй, правой линзы. Теперь постройте изображение
станет предметом для второй, правой линзы. Теперь постройте изображение 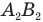 предмета АВ, в правой линзе. Это изображение
предмета АВ, в правой линзе. Это изображение 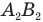 и станет окончательным изображение предмета АВ, даваемым этой системой линз.
и станет окончательным изображение предмета АВ, даваемым этой системой линз.
Величина D, обратная фокусному расстоянию, называется оптической силой линзы: 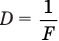 .
.
Оптическая сила линзы может быть положительной и отрицательной. Положительной считается оптическая сила собирающей линзы, а отрицательной — рассеивающей.
Расстояние от предмета до линзы d и расстояние от линзы до изображения f связывает с фокусным расстоянием линзы F и ее оптической силой D формула линзы

Если линза собирающая, но изображение в ней мнимое, то эта формула принимает вид:
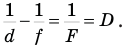
Если линза рассеивающая, то формула линзы принимает вид:
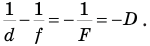
Если на линзу падает пучок сходящихся лучей, то точка их пересечения представляет собой мнимый предмет. В этом случае формула собирающей линзы с действительным изображением принимает вид:
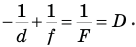
Увеличением линзы Г называют отношение линейного размера предмета к линейному размеру изображения:

Лупой называют короткофокусную собирающую линзу, предназначенную для относительно небольшого увеличения изображения. Рассматриваемый предмет помещают между фокусом и лупой, благодаря чему получают прямое и увеличенное изображение. Увеличение лупы определяет формула
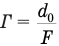
Здесь 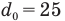 см — расстояние наилучшего зрения, F — фокусное расстояние лупы.
см — расстояние наилучшего зрения, F — фокусное расстояние лупы.
Если у человека нормальное зрение, то параллельные лучи, падающие на хрусталик глаза, пересекаются на сетчатке. При этом формула линзы имеет вид:

У близорукого человека параллельные лучи, упав на утолщенный хрусталик, пересекаются внутри глаза перед сетчаткой. Чтобы они пересекались на сетчатке, требуются очки со стеклами, аналогичными рассеивающей линзе. Применительно к глазу в таких очках формула линзы имеет вид:
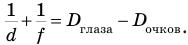
У дальнозоркого человека параллельные лучи, упав на хрусталик, пересекутся за сетчаткой. Чтобы восстановить зрение, требуются очки со стеклами, аналогичными собирающей линзе. Применительно к дальнозоркому глазу формула линзы имеет вид:
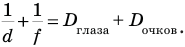
Если в условии задачи записано: оптическая сила рассеивающей линзы D = -4 дптр, то в предыдущую формулу подставляйте только модуль этого числа, т.к. минус в ней уже учтен.
Если линзы сложены вплотную, то оптическая сила системы таких линз равна алгебраической сумме оптических сил каждой линзы в отдельности — с учетом их знаков. Например, если сложили вплотную собирающую линзу с фокусным расстоянием  = 20 см и рассеивающую с фокусным расстоянием
= 20 см и рассеивающую с фокусным расстоянием 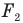 = 25 см, то оптическая сила такой системы линз будет равна:
= 25 см, то оптическая сила такой системы линз будет равна:
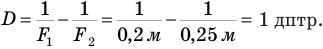
При вычислении оптической силы не забывайте переводить размерность фокусных расстояний — сантиметры в метры, иначе допустите грубую ошибку.
Если линзы расположены на расстоянии друг от друга, то определять оптическую силу или фокусное расстояние такой системы линз подобным образом — просто складывая оптические силы каждой линзы — нельзя. В этом случае фокусным расстоянием F такой системы линз является расстояние от последнего пересечения лучей, упавших на первую линзу параллельно ее главной оптической оси, до последней линзы.
Эта теория со страницы подробного решения задач по физике, там расположена теория и подробное решения задач по всем темам физики:
Возможно вам будут полезны эти страницы:

