Геометрическая интерпретация теории двойственности в задачах линейного программирования
Выберем задачу линейного программирования стандартного вида: минимизировать
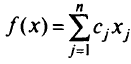
при условиях
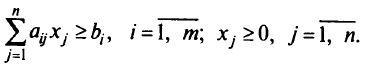
Пусть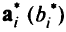 
при 
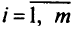совпадают с 
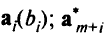есть единичный орт 
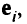а 
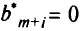при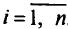 
. В разд. 1.3-1.5 мы видели, что обычное условие наличия безусловного экстремума функции во внутренней точке есть обращение в нуль градиента функции в этой точке.
Если при этом должны выполняться некоторые ограничения на переменные в виде равенств, то условием наличия экстремума в допустимой точке будет требование, чтобы в этой точке градиент функции и нормали к поверхностям, соответствующим ограничениям, были направлены «в одну сторону».
Более точно градиент функции в этой точке должен быть неотрицательной линейной комбинацией этих нормалей к поверхностям-ограничениям. В задаче линейного программирования каждое неравенство определяет допустимую область — полупространство. Для того чтобы допустимая точка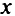 
была оптимальной, необходимо, чтобы градиент целевой функции в точке 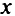выражался в виде неотрицательной линейной комбинации направляющих векторов тех и только тех ограничений, которые в точке 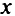обращаются в равенства, т.е. градиент целевой функции (вектор 
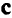) есть неотрицательная линейная комбинация нормалей векторов 
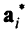для ограничений, обращающихся в равенство:
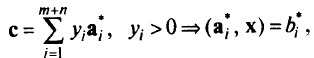
где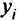 
— соответствующие коэффициенты линейной комбинации.
Из условий дополняющей нежесткости в слабой форме следовало: если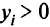 
, то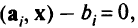 
, и если 
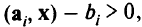, то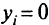 
.
В сильной форме утверждалось, что если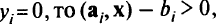 
, и если 
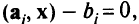, то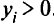 
.
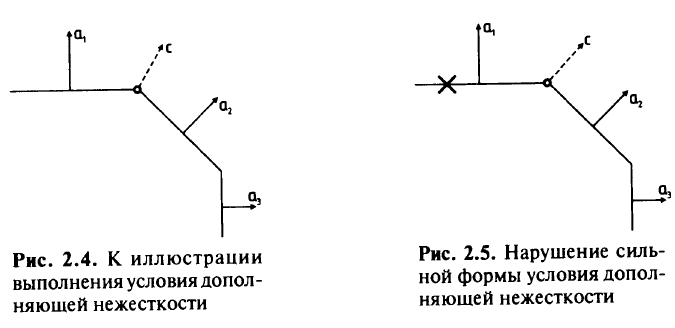
На рис. 2.4 изображены три гиперплоскости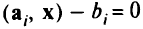 
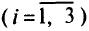и нормали к ним 
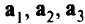. Если векторстакой, как показано на рис. 2.4, то он может быть выражен в виде неотрицательной линейной комбинации векторов 
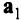и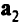 
; вершина, обозначенная кружком, соответствует оптимальному решению. Здесь
выполняются и условия дополняющей нежесткости как в слабой, так и в сильной форме:
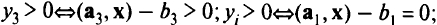
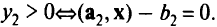
Если вектор с такой, как показано на рис. 2.5, т.е.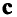 
— нормаль к одной из гиперплоскостей, 
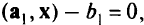,то оптимальная вершина в кружке не удовлетворяет сильной форме условия дополняющей нежесткости, поскольку 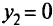и ,
и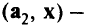 
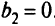. Но точка, помеченная крестом на рис. 2.5 и являющаяся оптимальным решением, удовлетворяет и слабой, и сильной формам дополняющей нежесткости:
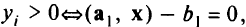
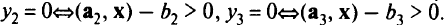
Для решения задач линейного программирования разработан так называемый двойственный симплекс-метод. Процедуру начинают с двойственно допустимого решения, когда одновременно
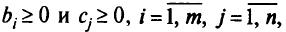
и сохраняют его двойственно допустимым на протяжении всех шагов. Он реализуется посредством таких же таблиц, как и прямой симплекс-метод. Но здесь сначала определяется, какая переменная должна быть выведена из базиса, а затем — какая должна быть введена в базис.
Всегда имеется возможность выбора: решать прямую или двойственную задачу, использовать прямой или двойственный симп-лекс-метод. Выбирают ту модификацию задачи, которую проще решать. Например, если исходная задача содержит переменные, на которые не наложено условие неотрицательности, тобываетудоб-нее решать двойственную задачу. Прежде чем записать двойственную задачу, полезно в исходной прямой задаче освободиться от ограничений в виде равенств, поскольку они будут порождать в двойственной задаче переменные, принадлежащие всей действительной оси.
В симплекс-таблице оптимального решения прямой задачи линейного программирования присутствует и решение двойственной к ней задаче. Чтобы это увидеть, надо элементы строки, где стоят коэффициенты целевой функции, представить в ви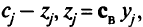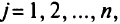де 
, где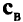 
— вектор, состоящий из коэффициентов целевой функции исходной задачи, стоящих в базисных клетках оптимального решения; 
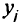— элементы 
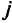-го столбца симплекс-таблицы оптимального решения, и добавить в симплекс-таблицу дополнительную строку 
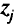. В строке 
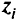в столбцах базисных переменных исходной задачи (обычно это последние 
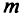столбцов) находится оптимальное решение двойственной задачи.
Таким образом, оптимальное решение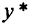 
двойственной задачи — это 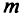последних элементов строки 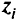оптимальной симплекс-таблицы прямой задачи; а оптимальным решением 
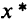прямой задачи — это 
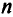последних элементов строки 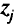оптимальной таблицы двойственной задачи.
В литературе, кроме того, описаны методы одновременного решения прямой и двойственной задач, например метод последовательного сокращения невязок
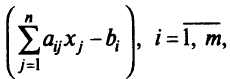
при фиксированных значениях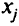 
.
Эта теория взята со страницы лекций по предмету «математическое программирование»:
Предмет математическое программирование
Возможно эти страницы вам будут полезны:
