Оглавление:







GAP напряжения генератора постоянного тока. Математическое описание
- Разрыв напряжения генератора постоянного тока. Математическое объяснение В качестве примера рассмотрим вывод дифференциального уравнения и передаточную функцию (см. Рисунок 1.4) системы автоматического регулирования напряжения (ATS) генератора постоянного тока. 2,24. Он состоит из электронного усилителя U, электродвигателя постоянного тока с независимым возбуждением D, которое является исполнительным механизмом, генератора G (цель, подлежащая настройке) и делителя напряжения DI, и его выходное напряжение рассчитывается из значения s0, заданного компаратором.
Давайте начнем с предмета регулирования. Генератор. Генератор управляется путем изменения переменного сопротивления Rn, включенного в цепь возбуждения (рис. 2.25, а). R „mH указывает его номинальное значение, то есть вы можете записать значение Rnt, где ток цепи возбуждения r является номинальным / v>. Отклонение DR переменного сопротивления пропорционально углу поворота вала двигателя + TEULr + 1) (Tyr + ) p (f) Wnf = kr2 из-за возмущения. Для передаточной функции замкнутой системы (относительно выхода DMg): px + o, p3 + Q> P- + <C P + a4, где ku = klk ^ Qq = ТяГемТв, я, = (7Я + 7В) ГЭМ1а2 = ^ м + ^ в. = Момент сопротивления Ms в P1 + ai P3 4- a2 p1 4- + a4 где = kR2 kTi Gy, bx = & d2 Lp1; гнев / U7. = U7, f (l + W) = ^ p ‘+ a ,,,’ — ^ -. ^ P) ^ Форма уравнения системы в символической форме (A0 p4 + a, p3 + fl2 P2 + o3P + a4) = KA0 — (^ oP + ^ i) Mc + + * r2 (a0p4 + a, p3-a2 p2 + ajj) /.
Сначала определим дифференциальные уравнения и передаточные функции для отдельных элементов в рассматриваемой системе. Людмила Фирмаль
Здесь Ci — положительная постоянная, а отрицательный знак указывает, что сопротивление Rn уменьшается, когда вал двигателя вращается в положительном направлении, и увеличивается, когда оно отрицательное. Следовательно, входное (управляющее) значение генератора — это угол (p, выход — падение напряжения u на нагрузке). Создание уравнений динамики генератора без учета влияния гистерезиса, вихревых токов и т. Д. 2.25 и б показаны эквивалентные электрические цепи генератора. Кроме того, защита и LB являются активным и индуктивным сопротивлением обмотки возбуждения (например, -emf). Генератор, ga — активное сопротивление обмотки якоря (игнорирование сопротивления игнорируется), RH — сопротивление нагрузки (при условии, что нагрузка активна).
E.s.generator связан с током возбуждения нелинейной зависимостью eT = F (iB), (2.116) Примерный график показан на рисунке 2.25, е. Дополнительный резистор R d выбирается таким образом, чтобы ток по сравнению с током нагрузки был незначительным. Тем не менее, вы можете написать: Для цепи возбуждения = (Br 4-Jap.n + AY) ‘in + LB dijdt, (2.117) Для якорной цепи em = (rj + rb) iat «r = f *„ <«(2-118) В статическом режиме при номинальных значениях тока возбуждения iB.u и якоря 1я.н эти уравнения принимают вид: «В n == (‘in + Dp.nK.n. (2.119) * gn = (^ i + /? n.n) ‘i.i,’ g.n = yav.n’ya.n- (2.120) Линеаризовать в рабочей точке, соответствующей номинальному значению тока возбуждения и якоря. (2.117) Присвоить i0 = iB.n + D * in и формулу (2.115).
- Откажитесь от подчиненных членов высшего порядка ξ | | | фφ от i, B, φ и рассмотрим (2.119) в Или символически где Ty = LJ (rB + H „.n) ki = ci iB.J (r линеаризация (2.116) где Используя это уравнение для ev и статическое уравнение (2.120), уравнение (2.118) можно преобразовать следующим образом: (2,123) Удалите D / d из (2.121) и (2.123) и, наконец, получите одно выражение, относящееся к входному (управляющему) φ и выходному количеству Aig, а также к возмущению генератора / = D / y. Два внешних воздействия (φ и /) применяются к генератору и представлены двумя передаточными функциями. Передаточная функция для управляющего воздействия и передаточная функция Wf с возмущением.
Для них: в форме оператора ^ +1). w, (p) = k P2, На изображении Лапласа W ^ (s) = kri / (TB 1), Wf (s) => kr2. На рис. 2.25, г показана структура генератора. Математическая модель генератора является пропорциональной связью для возмущений и апериодической связью (первого порядка) для управляющего поведения. Двигатель. На схеме приведена схема двигателя с независимым возбуждением. 2.26, а. При управлении со стороны якорной цепи напряжение возбуждения является постоянным. Рисунок 2.26, б, показывает эквивалентную принципиальную схему цепи якоря.
Где g и L — активное и индуктивное сопротивление обмотки якоря, // — ток якоря, а ed — эдс, индуцированная в обмотке якоря во время вращения. Людмила Фирмаль
Здесь мы делаем те же допущения об упрощении, что и при выводе уравнения генератора. Напишите уравнение якорной цепи # = С + (2,125) Э.д. е.а. пропорциональна угловой скорости двигателя с углом = C3d <p / dt. Значение постоянной с3 является током возбуждения и Структура двигателя. Выражение (2.125) можно преобразовать в следующую форму с учетом последнего выражения: г. или (Тир + I) * ‘+ pF = «■» меня Где Гя = -; — электрическая постоянная времени цепи якоря. ди (2,126) 1 ТяТенгр + Цмр + 1 1 Праведный Ву chyat9mp ‘+ temrch Рисунок 2.26.
Мистер вице-президент Может писать уравнения моментов на основе законов механики или Ur2F = MvR — Ms, (2,127) Где J — момент инерции вала двигателя (с учетом нагрузки). М№- крутящего момента. Ms — это момент сопротивления. Крутящий момент, пропорциональный току якоря Kp = c4i’tt. (2,128) Значение постоянной c4 зависит от тока возбуждения и конструкции двигателя, как и c3. Из (2.126), (2.127) и (2.128) магнитного резонанса момента и тока (I I J L 1 \ s, 1 (7> +1) -p2P + — / Является ли Ch-r pf = -mu. V C4 ^) Это уравнение (Тя7 \ mР2 + Т9Ыр + 1) RF = kxlиу-kl2 (Гяр + 1) Ме ((2.129) где Гем = Ogya / s3s4-электромеханическая постоянная времени; ~ Sz и -rJctc4 — передаточное число.
На изображении Лапласа уравнение двигателя имеет следующий вид: (T, Te> 1 s2 + r3Ms + 1) sΦ (s) = кМ Uy (s) — / rD2 (7> +1) / Is («) • (2.130) Где Uy (s) -L {uy}, Ms (s) = L {Ms}. Передаточная функция двигателя: Контрольным действием D1 LV1 IV / _ k (P) = —, Wu (s) = ‘(7-й тэй р «+ Tmr 4-1) р (Гр 79м с * 4 79мс 4-1) * Возмущение (момент сопротивления Ms) W (p) = ‘- +’) -, (ТяТ9Ыр ‘+ Т9ир + ) p w (S) = — * d «(Гя» + и-. (ГяГ9МS2 4-r9Ms + I) с Блок-схема показана на рисунке. 2.26, с, видно, что математическая модель двигателя может быть выражена. В виде возмущения, вызванного возмущением, вибрации (или двух апериодических, если T9M <.2 | / 7ГG9M) и управляющих воздействий серии-соединения-вибрации (или двух апериодических, если T9U <2 \ f TnT9M ) И цельные единицы.
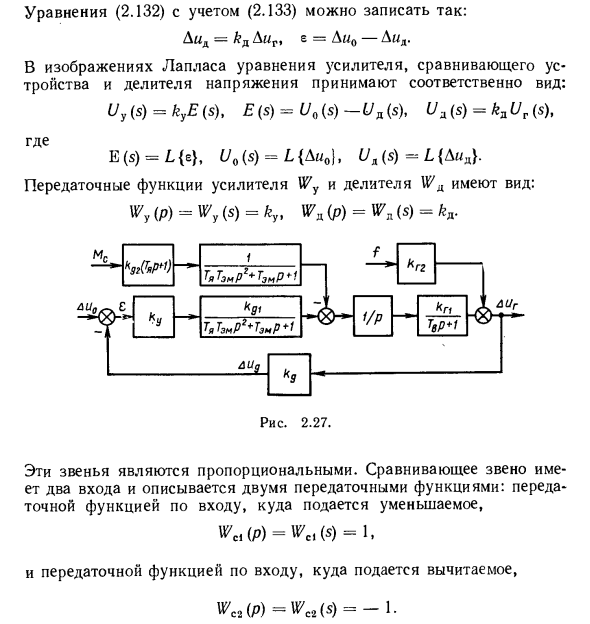
Усилитель, ссылка сравнения, делитель напряжения. Эти элементы описываются уравнениями uy = ky c, e = u0-id, id = ig, (2.131) Где ky — коэффициент усиления усилителя. CD — это «фактор деления» делителя. Линеаризованное уравнение генератора связывает отклонение ki с внешними воздействиями φ и /. Следовательно, уравнения одновременности (2.131) необходимо преобразовать, чтобы они зависели от отклонения Оленя (не yi). Запишите два последних уравнения (2.131) системы следующим образом: e = u0n + A «0- (» d.i + «d.n + = * d (» g.n + A «r), (2.132) Где yon, Md.n — установить номинальное значение действия и напряжение делителя, определяемое уравнением «Dn = K mg.n», он = «dn • (2.133)
Смотрите также:
Решение задач по теории автоматического управления
| Многомерные стационарные линейные системы | Определение устойчивости с помощью критерия гурвица |
| Нестационарные линейные системы | Критерии устойчивости Михайлова |

