Оглавление:












Г. Отрицательные температуры
- D. отрицательная температура До 1950 года абсолютные температуры считались существенно positive. In фактически, определение абсолютной температуры Кельвином (см. Главу 2,§ 1) связано с эффективностью цикла Карно. Е.= 1 —- <1、( D. 1.) 1 2 Это однозначно исключает возможность наличия объектов с негативом temperature. So, предполагая наличие отрицательной температуры, необходимо скорректировать формулировку закона 2-го Кельвина-планка (см. Главу 2,§ 1). в то же время, как показал Рамсей[33], формулировка Клаузиуса (см. Главу 2,§ 1) согласна с тем, что чем ниже температура 2-х объектов, тем выше температура, тем ниже абсолютная температура.
Если температура тела находится снизу вверх (слева направо), то получается следующая последовательность. Положительная температура:+ 0°, Г,+ 2°, -} — оо. Отрицательной температуре:—сотрудничество,. — 2°, −1°, −0°、 Поскольку необратимый переход тепла (энергии) от тела с отрицательной температурой происходит между телом с положительной температурой и телом с отрицательной температурой, неправильно расположить эти температуры в диапазоне от-su до+ oo, как при работе с вещественными числами. Неравенство. ^ + ^> 0. (D. Два)
Выразим второй закон термодинамики, который может быть выполнен только в случае Tu> 0 и T — <0 Сумма dQ — = dQ +отрицательна. Людмила Фирмаль
Поэтому необходимо учитывать, что объект с конечной отрицательной температурой»теплее», чем объект, находящийся при положительной температуре. В зависимости от этого, температура по возрастанию (слева направо)может быть: 4 0°、4-1°、+ 2°、…. + оо,—оо. ..、-2°、-1°、-0°。 Как мы видели, в обычном представлении термодинамики (например, в главе 3,§ 5) температура равна частной производной энергии по отношению к энтропии. (Г. З.) Поскольку формула Клаузиуса основана на 2-м законе термодинамики, Рамзи пришел к выводу, что в результате анализа аксиомы это равенство справедливо при отрицательных температурах. Самый простой способ-определить температуру как равную (G. Z. Is принять) и приблизиться к понятию отрицательной температуры.
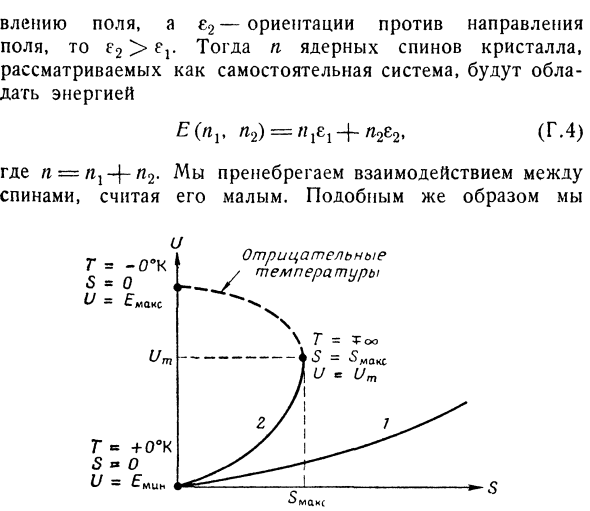
- Тогда внутренняя энергия делится на коэффициенты с частными производными (G. Z. соответствующее состояние — это состояние с отрицательной температурой, если (I)) может быть где-то в функции такой энтропии отрицательным, соответствующее состояние будет состоянием с отрицательной температурой. temperature. In для того чтобы система находилась в состоянии отрицательной температуры, необходимо ограничить энергию системы сверху. Состояния как минимальной, так и максимальной энергии Emax могут быть реализованы одним механическим состоянием, поэтому, согласно принципу Больцмана(см. Главу 2,§ 5), эти состояния должны соответствовать нулевой энтропии. При минимуме внутренней энергии£min <U <£max энтропия s (U)должна быть положительной и конечной. Типичная кривая у (Х) для системы, которая может быть в негативном температуры показана на рисунке 1. 26. В нормальной системе нет верхнего предела значения энергии, и функция U (S) монотонно возрастает.
Температура T = dUjdS всегда положительна (кривая/).Напротив, функция U (5 ′) имеет вид Вой 2, монотонно нарастающий только до точки Если энтропия достигает максимума 5 = 5max. At в этот момент производная dU / dS резко меняет значение с+ co на-co. Состояние энергии U% в диапазоне Um <U <£max в верхней части (пунктирная линия) Кривой 2 явно является отрицательным температурным состоянием. Для обеих кривых и=Åмш соответствует абсолютному нулю-для FO ° k-положительная температура (сплошная кривая), нет существенной разницы между состояниями, соответствующими кривым 1 и 2.At в то же время точки U = Umt S-SMax, Т = ±con Кривой 2 соответствуют кривым/верхним точкам Бесконечности U = oo, 5 = co, T = co.
Состояние, в котором соответствуют точки штриховой части кривой U (5), не похоже на обычное system. In в частности, следует отметить, что точка T-0°K указывает на состояние, наиболее удаленное от абсолютного zero. It следует также помнить, что нагрев системы до положительного температурного состояния не позволяет достичь отрицательного температурного состояния. Конечно, из-за увеличения энтропии она может подниматься вдоль ветви Кривой 2, что соответствует положительной температуре. То есть он нагревает систему и рассеивает в ней определенное количество энергии. it. In пунктирная часть кривой 2, можно только спуститься (по аналогичным причинам).Таким образом, состояние T—0°K равно、
По той же причине, что состояние Т— не может достигать + 0°К. Для обоих этих состояний можно сформулировать 3-й закон термодинамики, но нужно помнить, что состояние±0°К имеет одинаковую энтропию (равную нулю) и соответствует каждому максимальному порядку, но в 2 совершенно разных состояниях. Если вы не занимаетесь конкретным случаем, все эти соображения покажутся вам очень абстрактными. Поэтому попробуем объяснить упрощенную модель системы ядерных спинов, которая привела к открытию Паунда и Перселла [34]. Предположим, что энергия ядерного спина магнитного кристалла может иметь только 2 значения e и e2. £J соответствует ориентации магнитного момента в направлении* Поля, а r2-направление на поле, то e2> ev, то n ядерных спинов Кристалла, которые считаются независимыми системами, имеют энергию. Е(н Н2)= я-/ r2e2 (д. 4.)
Где n = nx — \ — n <2.Взаимодействие между спинами считается малым и игнорируется. Аналогично И фигура тоже. 26.Энергия как функция энтропии нормальной системы (кривая 1) и системы (кривая 2), где температура может быть отрицательной. Он игнорирует слабые взаимодействия между спиновой подсистемой и кристаллической решеткой. Какова неопределенность механического состояния, позволяющая использовать термодинамические описания? Очевидно, что если спин N1 параллелен направлению магнитного поля, то ситуация очень ясна, и поэтому энтропия равна нулю. Однако эта первая ситуация не меняется.
Таким образом, хотя вклад спин-спинового взаимодействия в общую энергию пренебрежимо мал, мы все же предполагаем, что NX параллельные и N2 антипараллельные спины помещают систему в статистически равновесное состояние, хаотично распределенное на участке решетки. Метод. Заданная энергия E (nv n2) равна、 Летучая мышь. Такое место. Предполагая, что время, необходимое для достижения этого статистического равновесия в спиновой системе(время спин-спиновой релаксации), очень мало по сравнению со временем спин-решеточной релаксации, система находится в состоянии термодинамического равновесия. Энтропия(согласно принципу Больцмана) 5 = к \ НК «н(д. 6.) «Энергия У = Е (Н Н2). (D. 7.) Сразу видно, что поведение системы должно соответствовать кривой фиг. このシステムの動作が図2の 曲線線2に対応す べきであることは。ぐに明らかである 26.In в частности, если все спины параллельны (n1 — n) антипараллельным (n2 — n) местам 2, соответственно Е =ШП= ОГ, Ш = с’х = 1, У = Е» у 5 = 0 Минут. И затем Э = нэ= Е^, Ж = С°П = 1% «2 ^Макс」 и = — ей а, 5 = 0. Теперь вы можете рассчитать температуру T-du’DS. Факториал и формулы (D. 4), (D. 6) и (D. 7)используя приближение Стерлинга, вы получаете следующее: ДС К Л, 1 / п ов — JTT7 = — в — = «тг.(D. 8.) Ди Е2-Н2 Т Х 7
- Паунд и Перселл достигли состояния отрицательной температуры в этом смысле, потому что они получили состояние равновесия при n2> nv. В первых экспериментах фунта и посылки спин первоначально был направлен в сильное магнитное поле. Затем, используя остроумный метод, мы поменяли взаимную ориентацию магнитного момента и магнитного поля. field. In в этом случае большая часть вращений направлена против поля. Спин-время спиновой релаксации
Температура, определенная таким образом, может быть положительной или отрицательной, в зависимости от того, является ли n1 или n2 большим. Людмила Фирмаль
В кристаллах LiF, по оценкам, находится порядка 10% сек. Время релаксации спиновой решетки составляет более 10 seconds. As в результате условия равновесия в подсистеме были четко соблюдены. Перепишите в следующем виде (д. 8.) П2. (D. 9.) Это частный случай Больцмана distribution. At положительная температура, население уровня n2 с более высокой энергией будет ниже: n2 nx%, то есть население выше более высокого уровня будет больше. Для усилительных устройств, таких как Мазер, инверсия соотношения населения уровня атомной энергии является общей.
При разговоре об обратной заселенности уровня иногда используется понятие отрицательной температуры, но это вопрос терминологии, так как инверсия соотношения заселенности еще не является состоянием отрицательным temperature. In для того, чтобы последнее произошло, инверсия соотношения популяций должна быть сохранена как равновесное состояние (почти) изолированной системы. Только в этом случае распределение Больцмана с использованием отрицательной температуры в качестве параметра (D. 9) имеет смысл.
Смотрите также:
| Преобразования Лежандра | Вводные определения |
| Якобианы | Экстенсивные и интенсивные переменные |