Постоянной величиной называется величина, сохраняющая одно и то же значение.
Переменной величиной называется величина, которая может принимать различные числовые значения.
Областью изменения переменной называется совокупность всех принимаемых ею числовых значений.
Переменная величина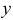 
называется функцией (однозначной) от переменной величины 
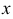, если каждому значению величины 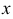, из области ее изменения, соответствует единственное вполне определенное значение 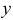или, в символической записи, 
.
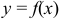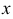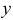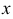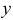Переменная называется независимой переменной или аргументом, иногда называют зависимой переменной. Относительно самих величин и говорят, что они находятся в функциональной зависимости. Символ 
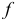называется характеристикой функции. Вместо буквы 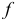можно употреблять любую другую букву. Частное значение функции 
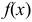при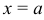 
записывается так: 
.
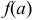Графиком функции 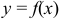называется множество всех точек 
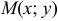плоскости 
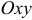, координаты которых связаны данной функциональной зависимостью.
Классификация функции одного аргумента:
1. Целая рациональная функция или многочлен
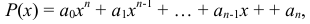
где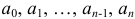 
— постоянные числа, называемые коэффициентами; 
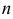— целое неотрицательное число, называемое степенью многочлена.
2. Дробная рациональная функция представляется в виде частного от деления двух целых рациональных функций
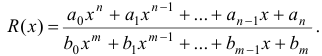
3. Иррациональная функция содержит возведение в степень с рациональным нецелым показателем. Например: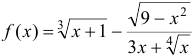 
.
Перечисленные три вида алгебраических функций образуют класс явных алгебраических функций. В общем случае алгебраической функцией называется любая функция 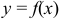, которая удовлетворяет уравнению вида
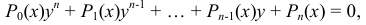
где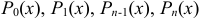 
— некоторые многочлены от .
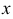Функция, не являющаяся алгебраической, называется трансцендентной.
Основные элементарные функции имеют области определения:
1) степенная функция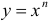 
или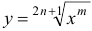 
определена при любых , 
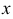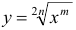определена в интервале 
(
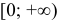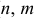— натуральные числа);
2) показательная функция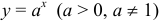 
определена при любых ;
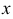3) логарифмическая функция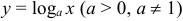 
определена в интервале 
;
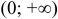4) тригонометрические функции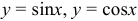 
определены при любых , 
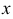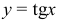определена 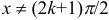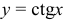при 
, 
— при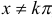 
;
5) обратные тригонометрические функции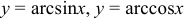 
определены на отрезке [-1; 1]; 
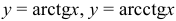— при любых .
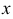Способы задания функции: аналитический (с помощью формулы), табличный (с помощью таблицы) и графический (с помощью графика).
Пример:
Задана функция:
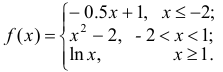
Найти точки разрыва функции, если они существуют. Сделать чертеж.
Решение:
Не элементарная функция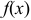 
определена на всей числовой оси. Она может иметь разрыв в точках 
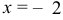и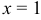 
, где меняется ее аналитическое выражение. Во всех остальных точках своей области определения функция 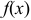непрерывна, поскольку каждая из формул, которыми она задана, определяет собой элементарную функцию, непрерывную в своем интервале изменения аргумента 
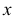. Исследуем точк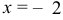и и :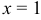
a)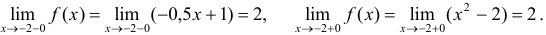 
Следовательно, в точке 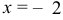выполняются все условия непрерывности, поэтому в этой точке функция 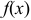непрерывна.
б)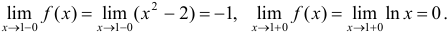 
Левый и правый пределы функции конечны, но не одинаковы, поэтому в точке 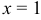функция имеет разрыв (конечный). Скачок функции в точке разрыва конечный 
.
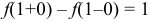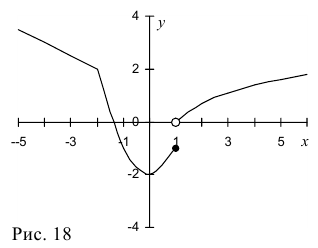
График функции приведен на рис. 18.
Ответ: функция имеет конечный разрыв в точке 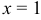, ее скачок равен 1.
На этой странице размещён краткий курс лекций по высшей математике для заочников с теорией, формулами и примерами решения задач:
Высшая математика краткий курс лекций для заочников
Возможно вам будут полезны эти страницы:
| Кривые второго порядка: эллипс, гипербола, парабола |
| Исследование общего уравнения кривой 2-го порядка |
| Вычисление пределов функции |
| Вычисление пределов от рациональной дроби при x > a (a ≠ ∞ ) |
