Оглавление:
Функция одной переменной. Наименьшее и наибольшее значение функции
Функция называется возрастающей в некотором интервале, если для любых двух чисел 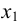 и
и 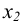 из этого интервала из неравенства
из этого интервала из неравенства 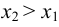 следует неравенство
следует неравенство 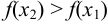 .
.
Если из неравенства 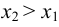 следует неравенство
следует неравенство 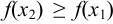 , то функция называется неубывающей в этом интервале.
, то функция называется неубывающей в этом интервале.
Функция  называется убывающей в некотором интервале, если для любых двух чисел
называется убывающей в некотором интервале, если для любых двух чисел 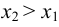 следует неравенство
следует неравенство 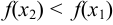 .
.
Если из неравенства 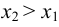 следует неравенство
следует неравенство 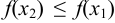 , то функция называется невозрастающей в этом интервале.
, то функция называется невозрастающей в этом интервале.
Функции возрастающие, убывающие, невозрастающие и неубывающие называются монотонными.
Следующая теорема выражает важный признак строгого возрастания и убывания функции и указывает правило для определения интервалов, в которых функция возрастает и убывает.
Теорема. Если во всех точках некоторого интервала первая производная 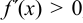 , то функция
, то функция  в этом интервале возрастает. Если же во всех точках интервала первая производная
в этом интервале возрастает. Если же во всех точках интервала первая производная 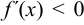 , то функция убывает в этом интервале.
, то функция убывает в этом интервале.
Правило. Для определения интервалов строгого возрастания и строгого убывания функции следует решить неравенства: 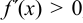 и
и 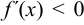 . Если окажется, что эти точки не заполняют сплошь какого-либо частичного интервала, то неравенства эти укажут интервалы строгого возрастания и строгого убывания функции.
. Если окажется, что эти точки не заполняют сплошь какого-либо частичного интервала, то неравенства эти укажут интервалы строгого возрастания и строгого убывания функции.
При решении задач, в которых требуется определить интервалы возрастания и убывания функции, следует, прежде всего, определить область существования этой функции.
Задача №64.
Найти интервал возрастания и убывания функции
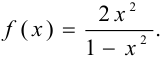
Решение:
Функция существует для любых 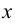 , кроме
, кроме 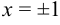 , т. е. областью существования функции являются интервалы
, т. е. областью существования функции являются интервалы 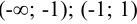 и
и 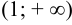 . Находим производную функции:
. Находим производную функции:
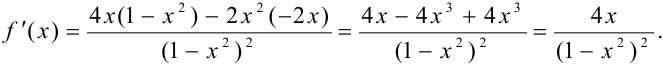
При 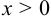 производная
производная 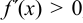 , при
, при 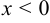
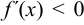 . В интервале
. В интервале 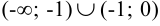 функция убывает, а в интервале
функция убывает, а в интервале 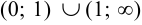 функция возрастает.
функция возрастает.
Говорят, что функция 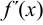 имеет в точке
имеет в точке 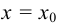 максимум, если значение функции в этой точке больше, чем её значение во всех точках, достаточно близких к
максимум, если значение функции в этой точке больше, чем её значение во всех точках, достаточно близких к 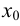 . Иначе, функция
. Иначе, функция  имеет максимум при
имеет максимум при 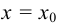 , если
, если 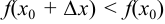 для любых положительных и отрицательных значений
для любых положительных и отрицательных значений 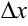 .
.
Говорят, что функция  имеет в точке
имеет в точке 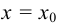 минимум, если значение функции в этой точке меньше, чем её значение во всех точках, достаточно близких к
минимум, если значение функции в этой точке меньше, чем её значение во всех точках, достаточно близких к 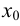 . Иначе, функция
. Иначе, функция  имеет минимум при
имеет минимум при 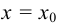 , если
, если 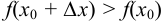 для
для 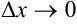 .
.
Если в некоторой точке функция имеет максимум или минимум, то говорят, что в этой точке имеет место экстремум, а точка называется экстремальной.
Необходимое условие экстремума. Если функция  имеет экстремум при
имеет экстремум при 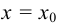 , то ее производная в этой точке равна 0 или
, то ее производная в этой точке равна 0 или 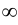 , или вовсе не существует.
, или вовсе не существует.
Точки экстремума функции следует разыскивать только среди тех, в которых её первая производная 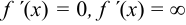 или
или 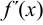 не существует. Эти точки называются критическими (если функция непрерывна). Это необходимое, но недостаточное условие существования экстремума.
не существует. Эти точки называются критическими (если функция непрерывна). Это необходимое, но недостаточное условие существования экстремума.
Этот материал взят со страницы кратких лекций с решением задач по высшей математике:
Решение задач по высшей математике
Возможно эти страницы вам будут полезны:
| Производная высших порядков задача с решением |
| Правило Лопиталя задачи с решением |
| Первое достаточное условие существования экстремума функции |
| Второе достаточное условие существования экстремума |

