Оглавление:
Функции нескольких переменных. Понятие функции нескольких переменных
Во многих вопросах естествознания приходится иметь дело с функциями двух, трех и более переменных.
Пример 10.1.
Площадь прямоугольного треугольника с катетами х и у может быть задана в виде функции 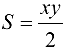 где
где 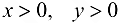 .
.
Пример 10.2.
Объем прямоугольного параллелепипеда с измерениями х, у и z представляет собой функцию 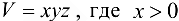 ,
, 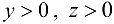 .
.
Пример 10.3.
Величина силы притяжения F двух материальных точек, имеющих массы 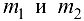 , и занимающих соответственно положения
, и занимающих соответственно положения 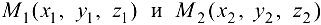 , согласно закону Ньютона задается формулой
, согласно закону Ньютона задается формулой 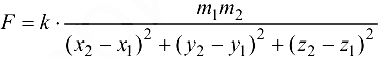 , где
, где 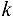 — некоторая константа, так называемая «постоянная тяготения».
— некоторая константа, так называемая «постоянная тяготения».
Определение 10.1. Если каждой упорядоченной совокупности значений переменных 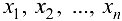 соответствует определенное значение переменной
соответствует определенное значение переменной 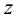 , то будем называть
, то будем называть 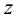 функцией независимых переменных
функцией независимых переменных 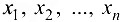 и записывать
и записывать 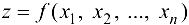 . В случае
. В случае 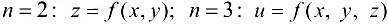 .
.
Замечание 10.1. Всякая функция от нескольких переменных (ФНП) становится функцией от меньшего числа переменных, если часть переменных зафиксировать, т. е. придать им постоянные значения.
Как и в случае одной независимой переменной ФНП существует, вообще говоря, не для любых значений 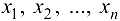 .
.
Определение 10.2. Совокупность наборов 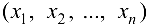 (точек
(точек 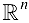 ) при которых определяется функция
) при которых определяется функция 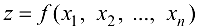 называется областью определения или областью существования этой функции.
называется областью определения или областью существования этой функции.
Область определения функции двух переменных представляет собой некоторое множество точек плоскости и наглядно иллюстрируется геометрически. Если каждую пару значений х и у изображать точкой 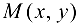 в плоскости
в плоскости 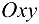 , то область определения функции будет представлять собой некоторую совокупность точек на плоскости. В частности, областью определения может быть и вся плоскость.
, то область определения функции будет представлять собой некоторую совокупность точек на плоскости. В частности, областью определения может быть и вся плоскость.
На практике изучаются случаи областей, представляющих часть плоскости, ограниченную линией. Линия, ограничивающая данную область, называется границей области. Точки области, не лежащие на границе, называются внутренними точками области.
Пример 10.4.
Найти область определения функции 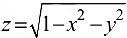 .
.
Решение:
Область определения функции будет задана условием 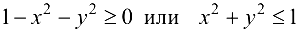 , т. е. представляет собой единичный круг с центром в начале координат.
, т. е. представляет собой единичный круг с центром в начале координат.
Определение 10.3. Геометрическим изображением или графиком функции двух переменных 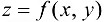 называется множество точек пространства
называется множество точек пространства 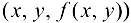 , определяющее, вообще говоря, поверхность в системе координат
, определяющее, вообще говоря, поверхность в системе координат 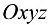 .
.
Геометрические изображения функций трех и большего числа переменных не имеют простого геометрического смысла.
Определение 10.4. Линией уровня функции 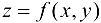 называется множество точек плоскости
называется множество точек плоскости 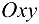 , для которых данная функция имеет одно и то же значение (изокривая).
, для которых данная функция имеет одно и то же значение (изокривая).
Таким образом, уравнение линии уровня имеет вид 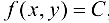 , где С — некоторая постоянная.
, где С — некоторая постоянная.
Пример 10.5.
Построить семейство линий уровня функции 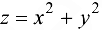
Решение:
Придавая z неотрицательные значения 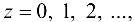 получим следующие уравнения линий уровня функции:
получим следующие уравнения линий уровня функции: 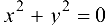 — точка О(0; 0);
— точка О(0; 0);
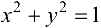 — окружность радиуса
— окружность радиуса 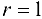 ;
;
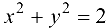
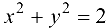 — окружность радиуса
— окружность радиуса 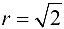 и т. д.
и т. д.
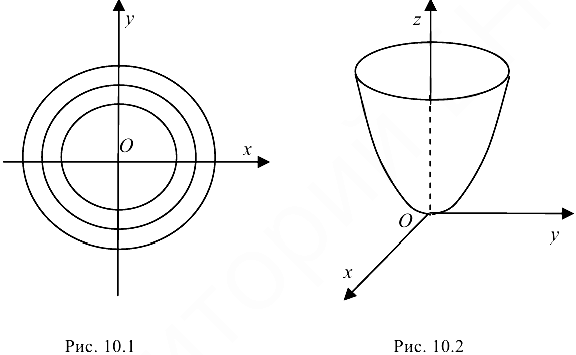
Таким образом, линии уровня данной функции представляют собой семейство концентрических окружностей с центром в точке  . Построив эти линии, получим «карту поверхности» для данной функции с отмеченными высотами (рис. 10.1).
. Построив эти линии, получим «карту поверхности» для данной функции с отмеченными высотами (рис. 10.1).
На рисунке видно, что функция 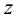 растет вдоль каждого радиального направления. Поэтому в системе координат
растет вдоль каждого радиального направления. Поэтому в системе координат 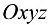 геометрический образ функции представляет собой гигантскую «яму» с круто растущими краями. Геометрически — это параболоид вращения (рис. 10.2).
геометрический образ функции представляет собой гигантскую «яму» с круто растущими краями. Геометрически — это параболоид вращения (рис. 10.2).
Определение 10.5. Поверхностью уровня функции 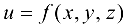 называется множество точек пространства
называется множество точек пространства 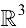 , для которых данная функция имеет одно и то же значение (изоповерхность).
, для которых данная функция имеет одно и то же значение (изоповерхность).
Линии и поверхности уровня постоянно встречаются в физических вопросах. Например, соединив на карте поверхности Земли точки с одинаковой среднесуточной температурой или давлением, получим изотермы и изобары, являющиеся важными исходными данными для прогноза погоды. Параллели и меридианы на глобусе -это линии уровня функций широты и долготы.
Эта лекция взята со страницы лекций по предмету математический анализ:
Возможно вам будут полезны эти страницы:

