Оглавление:
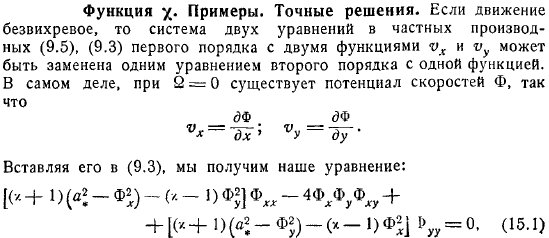

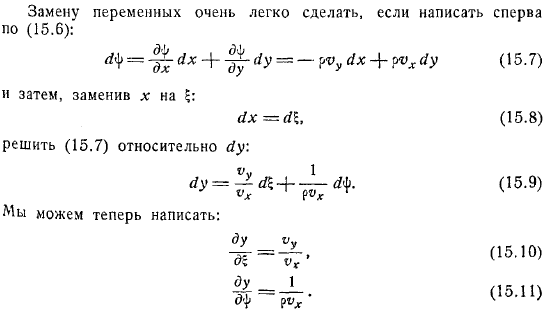





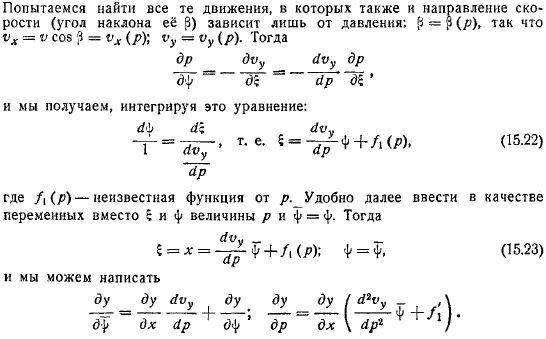
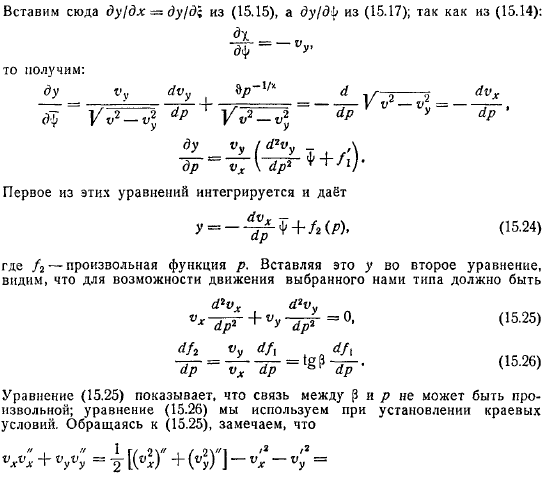


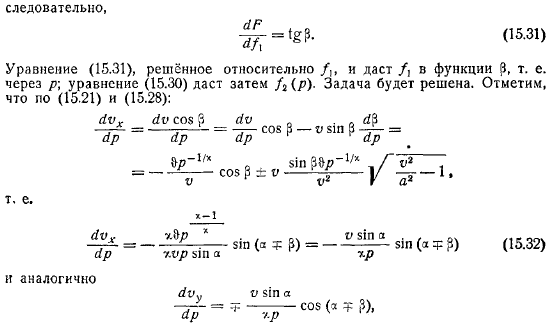
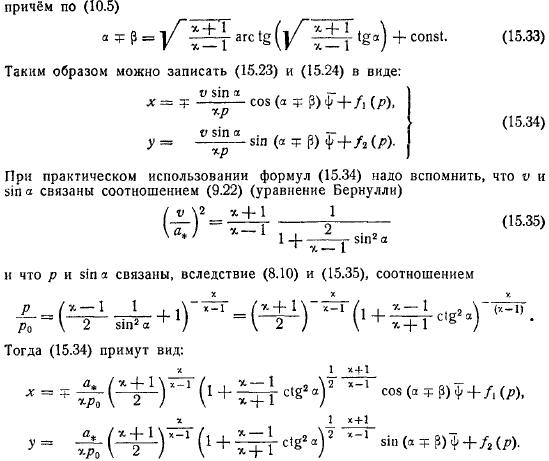
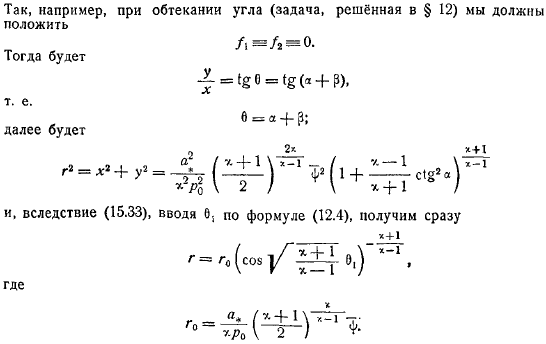

Функция. Примеры. Точные решения
Функция. Примеры. Точные решения. Факт, что существует потенциал для потенциала скорости. Если вы вставите его в , вы получите уравнение. Поэтому упражнение, которое мы ищем, возможно только на сверхзвуковых скоростях. Следующий , следовательно, если извлечь квадратный корень с обеих сторон, то получим.
Смотрите также:
Решение задач по гидромеханике
Но точно ли эта формула соответствует формуле и показывает взаимосвязь? И вдоль дороги характеристик. В результате, упражнение, которое мы ищем, будет одним из следующих: Вдоль характеристики выполнялись не только в полном диапазоне движения. Мы уже упоминали. Здесь решение может быть дано в закрытом виде. В настоящее время мы получили эти решения.
Смотрите также:
Если в движении нет вихрей, то систему первого порядка 2 уравнений в частных производных с 2 функциями можно заменить одним уравнением второго порядка с одной функцией. Людмила Фирмаль
Возвращаясь к определению, мы используем условие контура. Предположим, мы говорим о потоке вокруг контура, где конкретная функция. Заметим, что представляют собой параметрическое уравнение линии потока (параметр p). Скажем, на обтекаемой линии. Решенное уравнение относительно дает функцию . То есть через уравнение дает. Проблема решена.
Таким образом, вы можете написать и в следующей форме. Потому что, следует помнить, что при фактическом использовании формулы связаны (уравнение Бернулли). В этом случае принимает вид. Так, например, если она течет под определенным углом (задача решена) Тогда так и будет. Иначе говоря, больше будет, вводя 0 по формуле , вы получаете его сразу.
Смотрите также:
Дозвуковые скорости. Теория Чаплыгина. Примеры
Удобно пройти в переменную, если вы замените (которые не попадают под знак разницы) и уменьшите его, вы в конечном итоге получите простую формулу. Теперь вы можете легко создать одно уравнение, описанное. Функция делает вывод, что существует. Выражение можно записать в следующем виде, где должно быть выражено в следующей форме, основанной согласно уравнению Бернулли.
Задача о движение будет решена. Людмила Фирмаль
Формула может быть выражена с помощью в виде. Правая часть уравнения и не содержит функции y. Путем взаимного дифференцирования, мы получаем одну формулу для исключения y и определения функции y. Это формула выше. Всегда учитывайте 0 и заданную функцию.
Если определить функцию по формуле, то можно найти уравнения с помощью простого квадратурного метода. Но вы найдете обтекаемость плоскости (x, y) в функции у неизвестно и совпадает. Сейчас он принимает следующую форму: запустите основаны и зависят только от, прежде всего. То есть давление в разных линиях потока. Первое уравнение является интегральным и выглядит следующим образом.

