Оглавление:
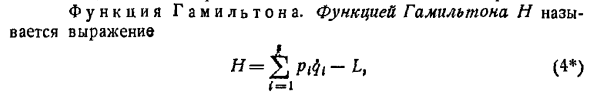





Функция Гамильтона
- Функция Гамильтона h является выражением 4 1. Где b t- Лагранжева функция кинетический потенциал, 5-число степеней свободы в материальной системе, обобщенная 1-я скорость, а p — обобщенный й импульс. Обобщенная скорость, содержащаяся в Гамильтоновой функции 4, должна быть выражена в соответствии с обобщенными координатами и обобщенным импульсом p1 см. Уравнение в обзоре теории в предыдущем разделе 3. Таким образом, в общем случае вид функции h равен h h, chp1, 5 Где 1, 2.
Гамильтонова функция, которая должна быть использована для создания канонического уравнения см .следующий абзац в этом разделе, имеет размерность энергии .Для стационарных связей, Гамильтонова функция H равна сумме механических энергий .З р п 6 Обобщенная скорость, содержащаяся в выражении кинетической энергии t выражения 6, должна быть выражена в соответствии с обобщенной координатой и обобщенным импульсом p1 см .уравнение 3 .Итак, если существует стационарная связь, то функция H зависит от обобщенных координат обобщенного импульса p а также не зависит явно от времени Ч, М 7 Где 1, 2, S .
Направим ось х параллельно оси пружины по горизонтали направо, взяв начало отсчета в положении ползуна, соответствующе. Людмила Фирмаль
Если на материальную систему накладывается нестационарная связь, то при составлении Гамильтоновой функции следует использовать формулу 4 .Для фиксированных соединений проще применить формулу 6 .в этом случае рекомендуется следующая последовательность действий 1 исследуйте число степеней свободы в материальной системе и выберите такое же число обобщенных координат .2 вычислить кинетическую энергию Т материальной системы .Она выражается в соответствии с обобщенными координатами и обобщенной скоростью .То есть T 1 1, 2, ..
Найти обобщенный импульс системы по Формуле 1, приведенной в обзоре теории предыдущего абзаца, и выразить их в виде функции обобщенных координат и обобщенной скорости 4 относительно решения системы уравнений, полученной в пункте 3 Обобщенная скорость, т. е. Получить Р, где 1, 2, ,. С 5 вычислить потенциальную энергию Р материальной системы. 6 Используйте результат абзаца. 2 и 5, Гамильтон вычисляет функцию 7 Г-ЛП 7 в Формуле h в предыдущем абзаце заменить обобщенную скорость с помощью зависимостей, полученных в 4. Задача 17.
Построена функция Гамильтона свободной материальной точки массы m, движущейся через гравитационное поле. Выберите декартовы координаты обобщенной точки. Решение. Задание 17. 7 а выполнили первые 4 пункта решения. Потенциальная энергия материальной точки П-Т 2. 1 Поскольку точка масс свободна, то Гамильтонова функция вычисляется по формуле, приведенной в обзоре теории 6. Задача 17. 7 используя уравнение 1 и уравнение 1 Ч Т П Т Л 5 л tyg. 2 Задача 17.
- Использует зависимость 3 для замены d и 7 в Формуле 2. Наконец, искомая функция Гамильтона принимает вид −2 p x y g n g- 3. Эта функция 7 зависит от обобщенного импульса px, pu, pg и обобщенных координат r. Задание 17. 10. Решите предыдущую задачу путем обобщения и получения сферических координат точек. Solution. In задание 17. 7 С, первые 4 пункта решения были заполнены. Энергия положения материальной точки p равна Н м. Р pco5b см. Рисунок b выпуска 17.
Важным моментом является бесплатным. Следовательно, функция Гамильтона равна его полной механической энергии, т. е. 7 7 p. Используя уравнение в вопросе 17. 7 7 и уравнение 1 77 м Р2 4-Р2 Р2 ы ПА в equal2 Т годовых, потому что 6. 2 Используя соотношение в вопросе 17. 7 9, заменив обобщенные скорости p, p и 6 обобщенным импульсом, остается Формула 2. Возьми И prgo d c080 — 3 Таким образом, искомая функция Гамильтона 3 зависит от обобщенного импульса pp, pf, pe и обобщенных координат p и b. Гамильтонова функция была вычислена по формуле h t 4-p. Это может быть применено в случае потенциальных сил и фиксированных coupling.
Для этого достаточно, воспользовавшись составленным дифференциальным уравнением движения, определить круговые частоты свободных н вынужденных колебаний и приравнять их друг другу. Людмила Фирмаль
Расчеты можно было проводить с использованием более общей формулы 4, приведенной в обзоре теории. Это выражение используется в нестационарной связи, в этом случае оно принимает вид 4 где i — p. Используя формулу 1 и формулу в вопросе 17. 7 7, запишем Б т-н 1 п Р2 Р2Р 81n2 8 Р23 — т р что. 5 5 если ввести результат в Формулу 4, то получится Я ППР rff4-pb8-г П24-pgf28t26 pg6g 8-8 6 Чтобы получить искомую функцию Гамильтона, замените обобщенную скорость на Формулу 17. 7 с помощью зависимости 9 задачи 6. После простого преобразования получим выражение 3. Если мы сравним 2 метода составления Гамильтоновой функции, то увидим, что для фиксированной связи эффективнее использовать формулу h t p.
Задача 17. 11. В случае консервативной материальной системы, находящейся под действием потенциальных сил и подчиненной неподвижной связи, Гамильтонова функция указывает, что она равна полной механической энергии, то есть h t — — p Решение. Прежде всего, следует отметить, что в случае фиксированной связи кинетическая энергия t является равномерной функцией обобщенной скорости 2-го порядка.
Коэффициент a является, вообще говоря, функцией обобщенных координат. .. .. Согласно теореме однородной функции Эйлера для квадратичных функций Читатели, не знакомые с Формулой 2, могут легко проверить ее правильность. Для этого необходимо использовать Формулу 1 для вычисления частной производной кинетической энергии t для обобщенной скорости 0b 0a. 1101 1202 2202 1201 a 0, ab01. .И замените эти значения развернутой левой частью выражения 2, то есть суммой dt l 37 l a .
Смотрите также:
Предмет теоретическая механика
| Уравнения Лагранжа первого рода | Канонические уравнения Гамильтона |
| Канонические уравнения Гамильтона | Первые интегралы канонических уравнений Гамильтона |

