Функциональная зависимость

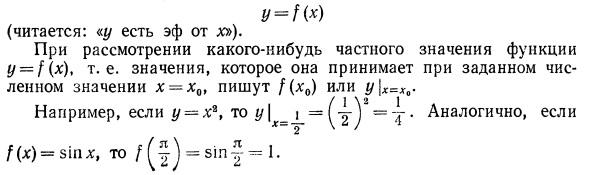
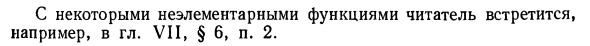
Функциональная зависимость

• Зависит от функции /. переменная Люди всегда должны соответствовать различным физическим величинам, таким как объем, плотность, длина, время, давление, температура и т. Д. Все эти величины качественно отличаются друг от друга, но могут быть измерены с течением времени. В результате измерения получается действительное число, которое называется числовым значением соответствующей величины. Если вы измеряете одну и ту же сумму, например, измеряете эту сумму в разные моменты или при разных условиях, вы можете получить разные цифры.

Точно так же давление определенной массы газа в герметичном контейнере имеет разные значения при разных температурах. Другими словами, само количество называется переменной, потому что числовое значение количества может измениться. Математика отвлекает от конкретного физического значения величин и рассматривает переменные (сокращенные переменные), данные, когда известны все возможные наборы чисел.

Например, скорости автомобиля на разных участках трассы или в разные моменты времени имеют разные цифры. Людмила Фирмаль

Постоянное значение (то есть значение, которое не изменяется в рассматриваемых условиях) считается частным случаем переменной, если набор чисел состоит из одного числа. Числа переменных образуют определенный набор действительных чисел. Соответствует определенному набору точек на оси значений. Оба этих набора могут быть очень разными (в зависимости от рассматриваемой переменной). Но в будущем вам, скорее всего, потребуется обработать ряд чисел, называемых сегментами и интервалами.

Решения. Область определения состоит из двух бесконечных интервалов (-oo, 2) и (2, + oo). Х- это x = 2 имеет смысл и определяется для всех других значений x. Читатель может легко понять, что когда функция y = xr, областью определения является вся ось значений, а когда функция y = x, x представляет собой бесконечный интервал x> 0. Обратите внимание, что невозможно различить функцию и выражение, в котором определена эта функция.

• Решение задач по высшей математике

Координаты на плоскости и в пространстве	Уравнение линии
Угол между двумя осями. полярные координаты	Преобразование координат

Примеры решения и задачи с методическими указаниями

Решение задач	Лекции
Сборник и задачник	Учебник

• Вы можете определить различные функции, используя одно и то же выражение. Фактически, в разделе 2 рассматривается область У (0, + oo) функции y-определения, а в разделе 3 представлена ​​функция y = -x * в области определения [-2,2]. Наконец, мы рассмотрели функцию, определенную только с выражением y = x2 без каких-либо дополнительных условий. Область этой функции — вся ось значений. Эти три функции отличаются друг от друга из-за разных определений домена.

Но они спрашивают Rns LG Используйте ту же формулу. Обратное также возможно, если одна функция в разных частях области определения задается разными выражениями. Например, рассмотрим функцию * /, определенную для всех неотрицательных значений x следующим образом: у = х равен 0 ^ х ^ 1, у = х2 есть х> 1, то есть J x, если \ x \, если x> 1.

График этой функции показан на рисунке. 18. Табличный способ установки функций. Когда определена табличная функция, создается таблица, которая показывает набор значений аргументов и соответствующие значения функций.

Эта функция определяется двумя аналитическими выражениями, которые влияют на разные части области определения. Людмила Фирмаль

Логарифмические таблицы, таблицы тригонометрических значений и многие другие широко известны. Во многих случаях необходимо использовать таблицу значений функций, полученных непосредственно из опыта. В следующей таблице показано удельное сопротивление р (Ом сантиметр) меди, полученной в результате экспериментов при различных температурах t (градусы). т 10 20 30 40 50 р! 810-дюймовый 1,8-S-6 1,9-10-дюймовый 2,0-S- * 2,0-S-6

/ 60 70 80 90 100 p 2,1-10 дюйма 2,2-U-6 2,2-10- * 2,3-10_ дюйма 2,4-U-® Графический способ определения функций. Когда задано графическое задание, указывается граф функции, и его значение, соответствующее тому или иному значению аргумента, извлекается непосредственно из этого графа. Часто такие графики строятся с использованием регистратора. 5. Основные основные функции и их графики Среди аналитически определенных функций основную роль нашего курса играют элементарные функции.

Сначала рассмотрим основные основные функции. Поэтому вызывается следующая функция: 1. Константа (постоянная) * / = C, где C — действительное число. 2. Степенная функция y = xn. Где n — ненулевое действительное число. 3. Экспоненциальная функция y = ax (a> 0; af1). 4. Логарифмическая функция y ~ loga * (a> 0, aF1). 5. Тригонометрические функции // = sin, v, y = cos l:, y = \ gx и [/ = ctgx. 6. Обратная тригонометрическая функция y = arcsin x, y = arccosx; y = arctgx; // = arcctgx. Рассмотрим области базового базового функционала и определения его графики. 1.

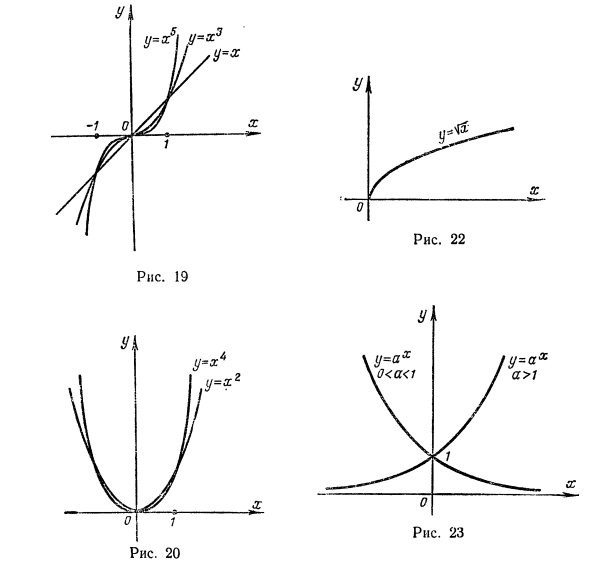
Константа — это функция, которая имеет одинаковое значение для всех значений своих аргументов. График функции y = C представляет собой прямую линию, параллельную горизонтальной оси. 2. Формат области определения степенной функции зависит от показателя степени n. Если n принимает другое натуральное значение, вы получаете набор функций y = x, y = ^ x2, y = x *, y = ^ x * и так далее. Доменом определения является вся числовая ось. Для нечетного n график показывает некоторые степенные функции. 19 и даже — рисунок 20.

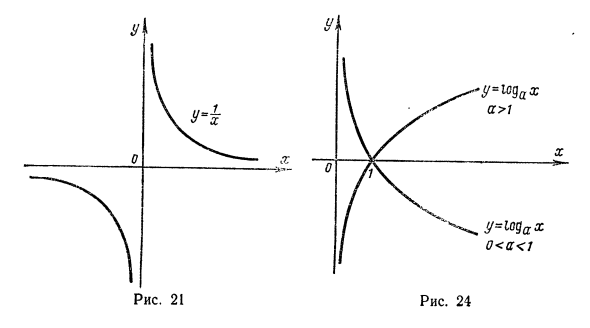
Из оставшихся степенных функций теперь рассматриваются только y = j (n = -1) и y = V до x = Их первый Y- ~ определен для всей оси значений, кроме точки x = 0. График этой функции показан на рисунке. 21. Вторая функция y —Yx (которая подразумевает корневое арифметическое значение) определена на графике, показанном на рисунке 5. 22.

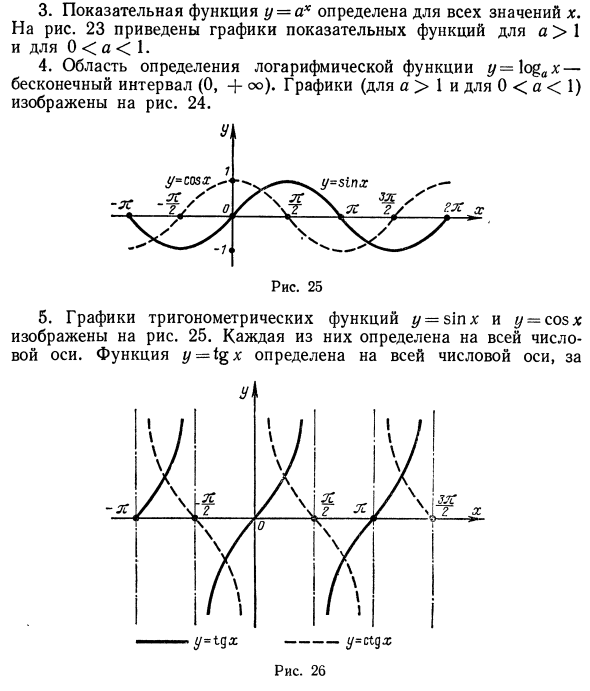
Экспоненциальная функция y = ax определена для всех значений x. На фиг.23 показан график показательной функции с a> 1 и 0 1 и O <a <1) показан на рисунке. 24. 5. График тригонометрической функции # = sinx и y-cos * показан на рисунке. 25. Каждый из них определяется по оси значений. Функция y-tgx определена для всей оси значений. -JC {1 / \ / \ / \ / / \ 1 Y f J к t 1 / \ / \ / Л / N sx -f X г ^ к о ^ у \ / \ / л / \ / \ / 1 РИСУНОК 26

-> — И функция y-ctxx является общей за исключением точки вида (2k + 1) За исключением точки x = — kn (k — произвольное целое число), показаны графики этих функций на оси значений. 26. 6. Ch — обратная тригонометрическая функция и ее график. V, §2, пункт 5. 6. Комплексные функции. Основные функции Ранее это было для функций, аргументы которых являются независимыми переменными. Однако во многих случаях вам нужно рассматривать аргумент как следующую функцию:Новая переменная функция. Рассмотрим функцию y = f (u). Аргумент является функцией переменной x.

В этом случае переменная y также является функцией от x. Эта функция называется составной функцией или функцией функции. Следующее отображается. «= Fl fM]. Переменные называются промежуточными аргументами для составных функций. Например, если * / = log, a = sin x, y имеет комплексную функцию x: (/ = log (sinx). При определении сложной функции мы предполагали, что у имеет функцию и. Следовательно, он принимает только те значения, для которых определена функция y = f (u). Однако значение x должно быть единственным значением, соответствующее значение которого попадает в область определения функции y = .f (u).

Например, логарифмическая функция определяется только для положительных значений аргумента, поэтому комплексная функция r = lg (sin x) определяется только для значений xy, где u = sinx> 0. Вы можете определить основные функции, используя концепцию сложных функций. Базовая функция определения — это одна базовая функция, которая использует четыре арифметические операции (сложение, вычитание, умножение и деление) и операцию, которая получает функцию из функции, которая применяется за конечное число последовательных раз. Функция, которая может быть определена аналитическим выражением. Основные базовые функции также относятся к базовому классу функций. Курс изучит основные функции точно, за редкими исключениями. Примером базовой функции является функция 0 = 18 (1 + «» * ), y = <■ «>, Y = U— 2 (* 3-Н) 5- * с Читатели, например, гл. VII, §b, пункт 2.

Определение 1. Интервал — это набор чисел x, удовлетворяющих неравенству а <х <б, Где а и б — действительные числа. Определение 2. Сегмент — это набор чисел x, удовлетворяющих неравенству Где а и б — действительные числа. Интервал обозначен символом (a, 6), а сегмент обозначен символом [a, b]. Кроме того, a и b называются соответствующим интервалом или концом сегмента.

Например, интервал (2, 5) состоит из всех чисел Xy, которые удовлетворяют неравенству 2 l: = 8 не принадлежат этому интервалу. Во многих случаях вам также необходимо рассмотреть набор чисел, которые удовлетворяют неравенству a a, спецификация (a, + oo); x ^ a, запись [a, + oo); x <b, запись (-oo, b); x <b, запись (-oo, b]. Вся ось значений также может рассматриваться как бесконечный интервал, обозначаемый символом (-oo, -} — oo).

Целые и дробные рациональные функции В этом разделе мы рассмотрим некоторые важные частные случаи основных функций. Определение Рациональная функция или целый многочлен является функцией вида y = a0xn + aixn’l + … + an-tx — \ — ant Где n — натуральное число, называемое полиномиальным порядком, aQt alt ap_g, а — действительное число, называемое коэффициентом Тами полином.

Пример рациональной функции: y = 2×3-1, y = xb-3×2 + 3x-1, y = 2x \ Полином первого порядка y = a0x + a1 называется линейной функцией. Замечания. Постоянная функция y = C может рассматриваться как полином нулевой степени: y = Cx °. Полином — это функция, определенная по всей оси значений. Определенная дробная рациональная функция или рациональная дробь — это отношение двух полиномов. Шиллинг (10) Вся рациональная функция является частным случаем дробных рациональных функций, где Q (x) постоянная. Соотношение фракций P (x) Основные функции определены для всех значений x, кроме тех, где знаменатель Q (x) исчезает. Примеры дробных рациональных функций: _ x2-3 * -1. _ x2— 1 x3 + 5 * a + 3, _ -у ~ х + 7; Y ~ х ‘

Функция четная и нечетная. Периодическая функция Некоторые из его свойств играют важную роль в функциональных исследованиях. В этом разделе мы рассмотрим четность, нечетные и периодические свойства некоторых основных функций. Функция определения y-f (x) вызывается даже для / (-x) -f (x) для x, принадлежащего области определения этой функции. Например, функции y ~ x2 и y = cos * являются четными числами. Это потому, что (-x) r-x2 и cos (-x) = cos x. Поскольку (-x) rk-x2k, показательная функция с четным показателем y = x2ky является четной

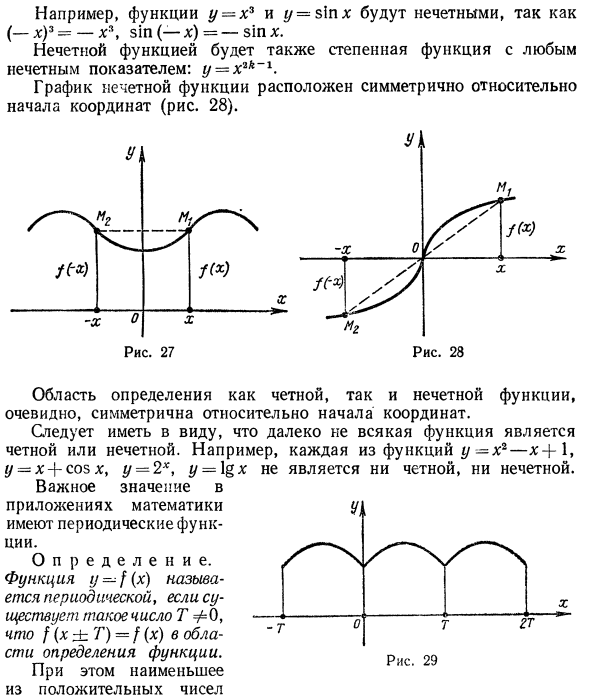
. Из определения четной функции видно, что две точки Mx (x \ [(x)) и Mg (-x; f (- *)) на графике этой функции симметричны относительно ординаты (рисунок 27). , Кроме того, поскольку x может быть произвольно выбран в области определения функции, график четной функции размещен симметрично относительно оси Oy (см. Графики для функций y = x2 и y = cos x на рисунках 20 и 25). ). Функция определения y-f (x) называется нечетной, если f (-x) = -f (x) для x, принадлежащего области этой функции.

Например, (-x) 3 = -x *, sin (-x) = -sin x, поэтому функции y = x3 и * / = sinx нечетны. Нечетная функция также является функцией, которая должна иметь произвольный нечетный показатель степени: y = x2k ~ 1. Графики нечетных функций располагаются симметрично относительно начала координат (рисунок 28). комната -T Рисунок 29 Область определения четных и нечетных функций явно симметрична относительно начала координат.

Имейте в виду, что не все функции являются четными или нечетными. Например, функция y —x2 — y —x-j-cosx, y = 2x, y = logx не четная или нечетная. Периодические функции важны в математических приложениях. Если в области определения функции определения существует такое число TΦ0, что / (xztT) = f (x), функция y-f (x) называется периодической. Кроме того, наименьшее положительное число

7 \ T удовлетворяет условию T) = f (x) y называется периодом Функциональный дом y = f (x) *. Из тригонометрии мы знаем, что функции f / = sinxt £ / = cosx, y-tgx и y-ctgx являются периодическими функциями. Их первые два периода — 2π, а последние два периода — i. При рассмотрении и построении периодической функции периода T достаточно знать значение этой функции в любом сегменте длины 7 \ (например, сегменте [0, 7 ‘]) (рисунок 29).

Другие значения для этой функции могут быть получены с помощью свойства периодичности этой функции. Например, если вы знаете значение функции (сегмент = [0,2π] / = s \ nx), вы можете легко получить значение этой функции для любого x (см. График функции * / = sinx на рисунке 25) ).Функциональная концепция Когда вы рассматриваете две переменные вместе, вы можете видеть, что значение одной переменной зависит от значения другой переменной. Например, площадь квадрата зависит от длины стороны. Когда x указывает длину стороны квадрата, а y указывает ее площадь, эта зависимость выражается как у = х \ Обратите внимание на две ситуации.

Знать набор чисел, который может взять х. Это набор всех положительных чисел. Фактически, x представляет длину стороны квадрата, поэтому он не может быть отрицательным или нулевым. С другой стороны, вы можете указать любое положительное число для x, потому что у вас есть право рассмотреть любой квадрат. 2. Поскольку x изменяется, y также изменяется, но согласно определенным правилам, каждое значение x соответствует определенному уникальному значению y.

Они говорят, что площадь квадрата зависит от длины его стороны. Давайте рассмотрим другой пример. Траектория s, по которой точка вещества движется линейно из точки A с постоянной скоростью v см / с, а через T секунд достигает точки B, точки до этого момента движения t s = vt. Где s является функцией от t. Опять же, 1) Значение, которое может принять t, известно. 2) Каждое из этих значений t соответствует одному значению s. Эти примеры можно обобщить следующим образом: Определение переменной y называется функцией переменной xy, когда: 1) Дан набор чисел М х. 2) Дается закон, где каждому значению x в этом наборе соответствует уникальное число y. В этом случае x называется независимой переменной или аргументом.

Если у является функцией от х, говорят, что между х и у существует функциональная связь. Определение Набор всех значений конкретного аргумента функции называется областью определения (или областью задач) этой функции. В первом примере выше область функции y = x2 была бесконечным интервалом (0, + oo). Во втором примере доменом функции s-at был сегмент [O, T]. Тот факт, что y имеет функцию переменной x, записывается символически следующим образом:у = ф (х) (Читайте: «у вас есть эффект х»). При рассмотрении конкретного значения функции y = f (x), то есть значение, требуемое для данного числа x = x0, записывается как f (x’0) или y \ x = x0. Например, если y = x2, y (g ^ * ==. Аналогично, f (x) = s \ nx, тогда = sin ~ = l.

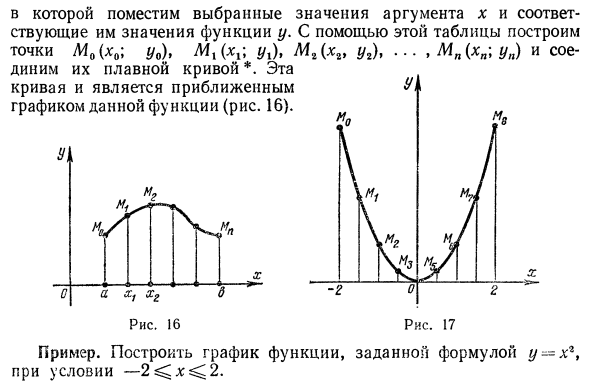
В дополнение к символу /, другие символы используются для обозначения функций. Например, y-φ (x), y к F (x), y = y (x). Точно так же функции и их аргументы не должны быть обозначены буквами y и x, они могут быть полностью указаны другими буквами. 3. график функции Во многих случаях, когда функция рисуется графически, то есть при построении графика, свойства функции более четкие и визуальные. График функции определения y = f (x) является геометрическим положением точки в плоскости Oxu, где каждая абсцисса x является значением аргумента, а ордината y является соответствующим значением этой функции. В общем, функциональные графики могут быть созданы на основе отдельных точек. Например, предположим, что функция * / = f (*) дана сегменту [a, b]. Выберите серию близких значений аргументов из a и b для построения таблицы X x0 = a * 2 xn = b Ву Ву

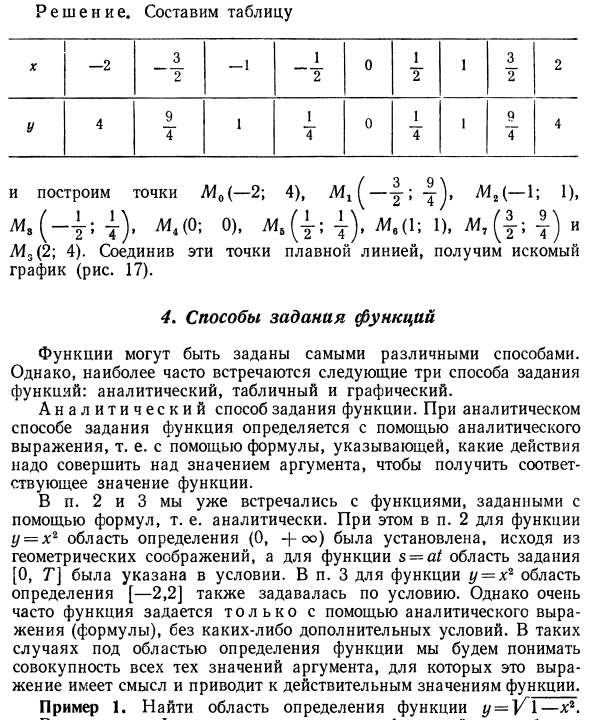
Помещает выбранное значение аргумента x и соответствующее значение функции y. Используйте эту таблицу для построения Пример. Создает график функции, заданной выражениями y к xr при условии-2 ^ x ^ 2. Решения. Давайте сделаем стол Х -2 3-1 1 0 1 1 3 2 2 2 2 2 y 4 9 1 1 0 1 1 Q 4 А 4 4 4 4 И построить точку M0 (-2; 4), Mx ^ — «J ‘m)’ — O» я> м «<0 ;?) • ^ г) и UI3 (2; 4). Соедините эти точки плавной линией, чтобы получить желаемый график (рисунок 17). 4. Как установить функции Функции могут быть установлены различными способами. Однако существуют три наиболее распространенных способа определения функций: анализ, таблица и графика. Аналитический способ настройки функций.

Метод указания функции аналитически использует аналитическое выражение, то есть выражение, которое указывает действие, которое должно быть выполнено над значением аргумента, чтобы получить соответствующее значение функции. вы. В §§ 2 и 3 мы уже встречали выражение, аналитически определенную функцию. Кроме того, гл. В 2 для функции y = x2 область определения (0, + oo) устанавливается на основе геометрических соображений, а для функции s область — [O, T] указывается в условии Это было В разделе 3 для функции y-x2 область определения [-2.2] также была задана условием.

Однако во многих случаях функции указываются только с использованием аналитических выражений (формул) без дополнительных условий. В таких случаях область определения функции означает полное значение всех аргументов, которые это выражение имеет смысл и приводит к фактическому значению функции. Пример 1. Функция y = V 1 — найти домен x2.

Решения. Функция задается только выражением, ее область определения не указана, и никаких дополнительных условий нет. Следовательно, в области определения этой функции нам нужно понять все значения аргумента x, где выражение V1 — x2 имеет действительное значение. Для этого вам нужно 1 — x2 ^ 0. Разрешение этого неравенства делает вывод, что областью действия этой функции является сегмент 1-1. ! ] • Пример 2 »Найти область определения функции Y =