Оглавление:






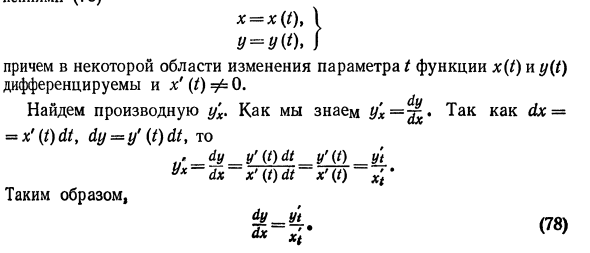



Функции, заданные параметрически, и их дифференцирование
- Функции, задаваемые параметрами и их отличиями /. Параметрические обязанности и линии До сих пор рассматривались линейные уравнения на плоскости, которые непосредственно связывают текущие координаты этих точек. Тем не менее, другой метод определения линий часто используется. В этом методе текущие координаты x и y считаются функцией третьей переменной. Укажите две функции переменной /. (73) То же значение / считается.
Когда переменная t проходит через все значения области функции (73), точка My) описывает конкретную линию C в плоскости Ohu. Уравнение (73) называется параметрическим уравнением этой линии, а переменная / называется параметром. Предположим, что функция x = x (() имеет обратную функцию / = φ (:) :).
Тогда одно из этих значений t соответствует однозначному значению x и однозначному значению y, так что определенная точка M (x \ y) соответствует. Людмила Фирмаль
Подставляя эту функцию во второе выражение (73), выражение (74) y = y [Φ (A ‘)], Выразите y как функцию от x. Я согласен, что эта функция параметрически определяется уравнением (73). Переход от этих уравнений к уравнению (74) называется исключением параметров. При рассмотрении функциональности, Найдите вторую производную. Второй по определению FX. ~ Dx2 рф * ‘дх Функция параметра- = / (/), DY \ дх) дх d ^
Следует рассматривать как заданную функцию Параметрический: 1 * = «(/). J ■ ‘8 Следовательно, ~ = определяется уравнением (78) вместо y ду Должен быть заменен (А ты (79) «» Dar Пример 3. Найти вторую производную функции y, определенной параметрически. x = sin2 /, ^ y = sin2 /. ) Решения. В примере 1 первая производная была найдена, но рассматривают эту производную как параметрически определенную функцию. | = 2ctg2 /, | я Пой- ^ 7.
| Производные высших порядков | Векторная функция скалярного аргумента |
| Дифференциал функции | Некоторые теоремы о дифференцируемых функциях |
Примеры решения и задачи с методическими указаниями
| Решение задач | Лекции |
| Сборник и задачник | Учебник |
- Согласно уравнению (78) * = найти sin2 /, вторая производная dyV ‘2 2 «в уравнении (79) Y / (2 ctg _ sin * 2 / __4 dx2 «» *
* (sin2 /) ‘~ 2 sin / cos /sin * 2 /’ \ Когда вы указываете параметр, исключение параметра не только не требуется, но и не всегда возможно на практике. Во многих случаях гораздо удобнее запрашивать разные значения для параметров и использовать уравнение (73) для вычисления соответствующих значений для аргументов x и y. Давайте посмотрим на некоторые примеры.
Пример 1.Декартовы координаты x и y этой точки выражаются полярным радиусом r-R и полярным углом. , §3, пункт 3): x = Rcostt \ y = Rs \ nt. ((7 ° Уравнение (75) называется параметрическим круговым уравнением. Эти параметры являются полярным углом / и варьируются от 0 до 2n. Если уравнение (75) возводится в квадрат и заканчивается для каждого члена, тождество устраняется тождеством cos2 // fsin2 / = 1, а круговое уравнение в декартовой системе координат xx + y2z = R * f определяет две основные функции вы: И tj- * / R2-A2’2. Каждая из этих функций определяется параметрически уравнением (75), но диапазон изменения параметров для этих функций различен.
Пусть M — любая точка на окружности с центром в начале координат и радиусе R. Людмила Фирмаль
Их первый 0 <t ^ i; график этой функции — верхний полукруг. Для второй функции Внизу находится нижний полукруг. Пример 2. Придумайте эллипс одновременно L, L -4 — = 1 a3 h b ‘1 Круг с центром в начале координат и радиусе а (рис. 138). Свяжите каждую точку M эллипса с точкой N окружности, которая имеет ту же абсциссу, что и точка M, и расположена одна за другой. Ось сторона ах. Положение точки N и, следовательно, точки M полностью определяется полярным углом t точки N. Кроме того, для этих полных абсцисс х мы получаем x- стоимость.
Найти ординату точки M из эллиптического уравнения. Y — V £ L \ в фа К в л з Рис. 138 Ордината точки M и ордината точки N y1 = a $ \ r \ t должны иметь один и тот же знак, поэтому выбирается знак «+». Таким образом, для эллипса получено следующее параметрическое уравнение: (76) Здесь параметр t изменяется от 0 до 2π. Пример 3. Рассмотрим окружность с центром в точке 01 (0; a) и радиусом a, который четко соприкасается с горизонтальной осью начала координат (рис. 139). Предположим, этот круг вращается, не скользя по абсциссе.
Затем точка M окружности, совпадающая с началом координат в первый момент, рисует линию, называемую циклоидой. Рис. 139 X При перемещении фиксированной точки из положения O в положение M параметрическое циклоидальное уравнение получают с использованием угла поворота MSW окружности в качестве параметра t. Далее, получите следующую формулу для координат х и у М: x = OL = OB — AB = OB — MD] y = LM = BD = BC — DC. Поскольку круг вращается вдоль оси Ox без скольжения, длина отрезка OB равна длине дуги VM. Поскольку длина дуги VM равна произведению радиуса a на центральный угол t, VM = at. Следовательно, OB = at. Где BC — a, MD = as \ nt, DC = стоимость. так x = at-as \ ntt y — a — cos /, или = a (t-sin /), 1-a (\ -cos /), j х = у (77)
Эти уравнения являются циклоидальными параметрическими уравнениями. Если параметр t изменяется от 0 до 2jx, круг совершит один полный оборот. Точка М в этом случае представляет собой одну арку циклоиды. Исключение параметра t делает здесь выражение громоздким и непрактичным. Параметрические линейные назначения часто используются, особенно в механике, где время является параметром.
Пример 4. Определите траекторию снаряда, выпущенного из пушки с начальной скоростью v0 под углом а от горизонтали. Сопротивление воздуха и размеры снаряда игнорируются, поскольку они считаются важными. Выберите систему координат. Для начала возьмем отправную точку снаряда от морды. Расположите его в той же плоскости, что и ствол пистолета, с горизонтальной осью Ox и вертикальной осью Oy. Без гравитации снаряд движется по прямой линии, образуя ось Ox и угол a, и путь vQt проходит к моменту времени t.
Координаты снарядов в момент времени t равны: x = cos a, y-v0t sin a. Из-за гравитации Земли, снаряд должен падать вертикально в этой точке Арканзас По значению ~. Таким образом, на практике, в момент времени t, координаты снаряда определяются x = v0t cos a, \ y-v0t sin a— ^ • J W В этих уравнениях u0, a и g — постоянные величины. При изменении t координаты хны точки запуска также изменяются. Уравнение () является параметрическим уравнением траектории снаряда, параметром которого является время t. Выразить из первого выражения () / = —— и присвоить ему VQ Cos GC
Второе уравнение получает уравнение траектории снаряда в виде tj = x-t% a ~~ 2vlc s ° a X. Х — параболическое уравнение. 2. Дифференцирование параметрически определенных функций Предположим, что функция y от x задана параметрически уравнением (73). х = х (т), \ у — у (т)> я Кроме того, в конкретной области изменения параметра t функции x (t) и y (t) дифференцируемы и x ‘(/) Φ0. Найдите производную y’x. Как вы знаете, yx = ^ 6 * dx = = x ‘(t) dt, dy = y’ (t) dt, то > dy_y ‘(t) dt y’ (t) yt yx dx x ‘{t) dt x’ (0 x’t ‘ Вот так ты не поймешь / * 7о \ Уравнение (78) находит производную параметрически определенной функции.
Пример 1. Найти производную функции y от k, заданную параметрическим уравнением x = sin2 /, \ y = sin2 /. Решение. Из уравнения (78) dy_y’t _ (sin 2Q ‘_ 2cos21 0 0 dx to x; (sin54 /)’ 2 sin / cos / ^ 8 Пример 2. Найти касательные и циклоидальные нормальные уравнения (А = 1) x = / -sin ^ r / = 1-cos / / T ~ Y ‘решение в точке Ml (xr; yx), соответствующей значению параметра. Найти координаты контакта Mt (xx \ yv). т. , Зло зла зло. Зло | -2 *! = (/ -Sin /) / = zy = -2 — Sin-2- = -2- + 1 * зло yt = (\ -cos /) = 1 — COS— = 1. • г Найти производную от уравнения (78), чтобы найти коэффициенты тангенса и нормального угла. dy_ (1-cos /) ‘_ sin t dx ~ (/ -sin /) ‘~~ 1 —cos /
Найти угловой коэффициент касательной к циклоиде в точке М. b-dJ-1- (sin / \ = —I * kas- <fx | Af, -U-cos /;! Ev / = т И нормальный угловой коэффициент K = -f— —1 ■ «СУО Используя уравнение прямой через данную точку, Y — Yx = b (x — xx), Легко получить касательные уравнения ,. (Zl + 2 \, Zl-A и y — — b ^ x-J-J или l: — И нормальное уравнение -1 = 1 Или X — y — y = 0. Уравнение (78) можно использовать для нахождения производных высшего порядка функции, определенной параметрами. Покажи как

