Функции состояния

Функции состояния

• Государственная функция Теперь мы дополним рассмотрение 1-го и 2-го законов, используя некоторые математические факты, известные из обычного анализа. Во-первых, рассмотреть общие формы Пфаффа производной с 2 переменными ДЗ = Р(х, у) ДХ + г(х, г)ды. (2.59） В некоторых случаях То есть, если P и Q удовлетворяют условию интегрируемости Как вы знаете, dz-это идеальная производная、

Линейный Интеграл J dz между 2 точками xxx и x2y2 не зависит от пути в xy plane. In в частности, Интеграл пути равен нулю § ДЗ =0.(2.62） Мы использовали этот факт в§ 3, чтобы указать, что энтропия S = J dQ06plT является функцией Государство. Поглощение тепла Q = J dQ и полное И наоборот, работа L = J PdVt не является функцией

состояния, даже если это обратимый процесс. Это можно проверить сразу, рассмотрев 1 различные (обратимые) процессы a и b (см. Рисунок 7) от 1 состояния (1) до 2 различных состояний (2).Для обработки、 Два ОК => \ йд = У2-УБ + Ла(2.63） Я… (ля） И процесс B Два Дь = Дж йд = У2-УБ + ЛБ. (2.64)） л. Ф） Рисунок 2 7. в общем, вы можете видеть, что работа, выполненная в процессе a, соединяет одно и то же начальное состояние 1 и конечное состояние 2, в отличие от работы, выполненной в процессе B. Ла = J Р дв Ф ЛБ = | Р дв. (2.65)） а б.

Поэтому следует отметить, что dQ и dL не являются полными различиями. Людмила Фирмаль

Следовательно, Qa ^ Qb.  1.Температура как интегральный делитель. Мы снова напишем первый закон термодинамики процесса, который влечет за собой бесконечное изменение параметров. йд = ду-у-дл. Если процесс обратим, то dQo6 = dU + PdV = = [г) ДТ + [(ж)т + п] ш = МДТ + НДВ (2.66） Где (dU / dT) v = M и{dUjdV) TP = N. правая часть уравнения(2.66) находится в терминах производных

dT и dV%, в Пфаффианской форме, но dM [dVΦdNjdT, поэтому она не может быть интегрирована. Для 2 независимых переменных всегда можно найти интегральный коэффициент[n (V \ V) t, например: ПЦО _ Д \ в ом Р7 \ И это оказалось совершенно по-другому. Распространяться В идеальном газе, который является формулой для частного случая (2.66)-m = const, N-RTlV, вы сразу увидите, что интегральный коэффициент равен| i = 1 /Г. Если принять во внимание обратимый

процесс сложной системы, состоящей из идеального газа и любого объекта в равновесии, то можно доказать, что эта форма универсальна. Однако, dQo6p! Поскольку T = dS уже указывает, что он всегда является совершенной производной (см.§ 3), он не выполняет это доказательство здесь. Решая уравнение в частных производных Jl1 ″ м + Гл)р + п} ^ — < > <2-68> Таким образом, 1 параметр » S С(в, Т) = const и = С.(2.69） Особенно в случае идеального

• газа, где требования (Щ —^® Мы получаем dS = Cvd в T + Rd в V.(2.70） Или Ы = ЦВ(телеканал «1» 1) — fпостоян. Кривая 5 = const описывается тем же дифференциальным уравнением(1.31) и(2.68), что и изоляция, рассматриваемая в пункте 1 раздела 1§ 4.Таким образом, эти 2 Поскольку обратимый процесс термоизоляции удовлетворяет условию 5 = const, набор кривых идентичен и Энтропия может быть выбрана в качестве параметра для определения кривой. Generalization. In выше мы рассмотрели простейший случай, то есть

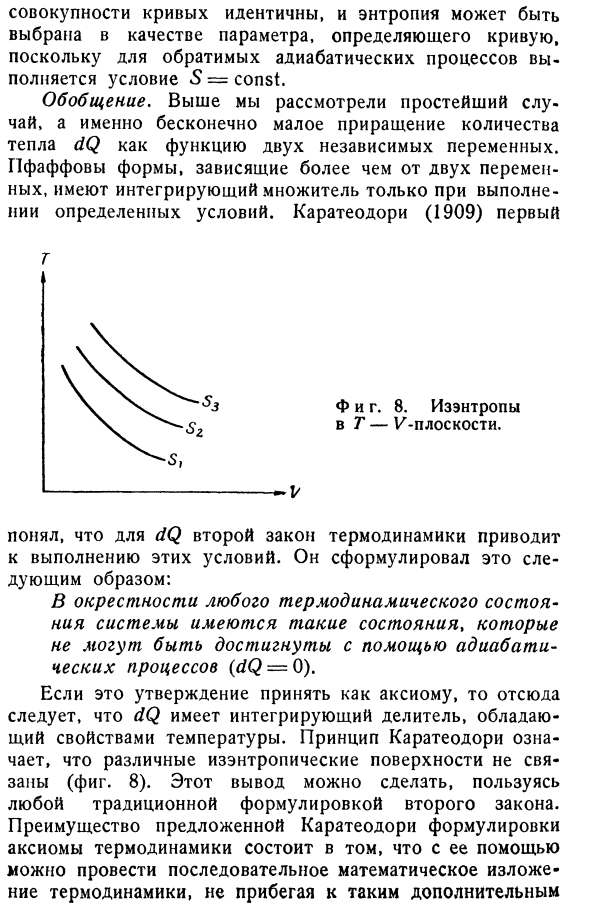
небольшое увеличение количества тепла dQ в зависимости от 2 независимых переменных. Форма Пфаффа, которая зависит от более чем 3 переменных, имеет интегральный коэффициент только при соблюдении определенных условий. Каратаодори (1909) первый Т. И фигура тоже. 8. А так-энтропия г-к плоскости. В. в случае dQ мы заметили, что 2-й закон термодинамики приводит к реализации этих условий. Он сформулировал следующее: Вблизи термодинамического состояния системы существует состояние,

которое не может быть достигнуто с помощью процесса теплоизоляции (dQ = 0). Если это утверждение принять как аксиому, то dQ имеет интегральный делитель с температурными характеристиками. (рис.8).Этот вывод можно сделать, используя традиционную формулировку второго метода. Преимущество формулировки

Принцип калатеодоритов подразумевает, что различные изоэнтропические плоскости не связаны между собой Людмила Фирмаль

аксиомы термодинамики, предложенной калатодри, состоит в том, что с ее помощью можно выполнить последовательное математическое выражение термодинамики, не прибегая к таким дополнениям. Концепция как полный цикл газа или Карно. С другой стороны, презентация будет очень абстрактной. Попросите читателя обратиться к работе Борна, чтобы ознакомиться с методом каллате Тори[12].

Смотрите также:

Предмет термодинамика

Примеры	Примеры и приложения
Энтропия и вероятность	Макроскопическое движение