Оглавление:
Повторим важнейшие сведения о функции:
Если каждому значению переменной х из некоторого множества D соответствует единственное значение переменной у, то такое соответствие называют функцией.
При этом х называют независимой переменной, или аргументом, у — зависимой переменной, или функцией.
Множество всех значений, которые может принимать аргумент, называют областью определения данной функции и обозначают буквой D.
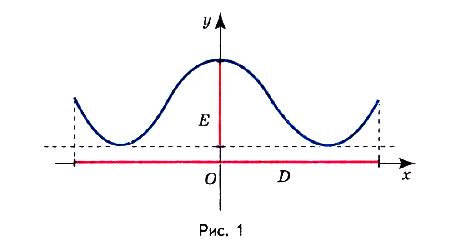
Множество всех значений у, которые может принимать функция, называют областью значении и обозначают буквой Е (рис. 1).
Две функции считаются разными, если у них разные области определения или правила соответствия. Например, функция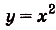 
заданная на промежутке [-3; 3], и функция 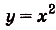, заданная на R, разные. А заданные на R функции 
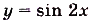и 
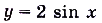
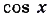одинаковые, поскольку выражения 
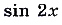и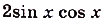 
тождественно равны.
Чтобы задать функцию, достаточно указать её область определения и правило соответствия. Если область определения не указывают, то считают, что она такая же, как и область допустимых значений формулы, которой задаётся функция.
Задавать функции можно разными способами: формулами, таблицами, графиками и т. д.
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты — соответствующим значениям функции.
Графический способ задания функции удобен своей наглядностью. Глядя на график, сразу можно оценить функцию, которую он задаёт, т. е. выявить её важнейшие свойства: найти область определения, область значений; выяснить, является ли данная функция периодической, чётной или нечётной; найти точки пересечения графика функции с осями координат и интервалы знакопостоянства; определить промежутки возрастания или убывания.
Если функция задана графически, то область определения функции — проекция её графика на ось Ох; область значений — проекция её графика на ось Оу (см. рис. 1)
Функция называется чётной(нечётной), если область её определения симметрична относительно числа 0 и для каждого значения х из области определения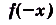 
.
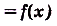
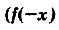
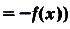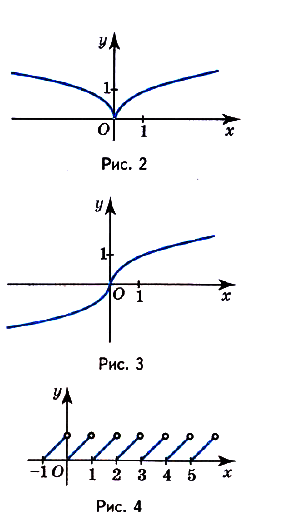
График чётной функции симметричен относительно оси Оу (рис. 2), а нечётной — симметричен относительно начала координат (рис. 3).
Например, из функций, заданных на R,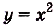 
,
,
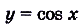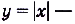чётные,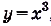 
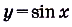— нечётные, а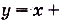 
, 
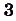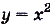
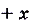ни чётные , ни нечётные.
Функция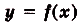 
называется периодической с периодом 
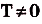, если для любого х из области её определения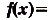 
.
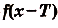
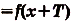График периодической функции с периодом Т отображается на себя параллельным переносом на расстояние Т вдоль оси Ох (рис. 4). Функци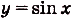и
и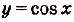 
периодические с наименьшим положительным периодом 
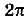, а функци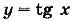и 
и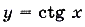 
— с наименьшим положительным периодом
.
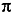Область определения периодической функции — вся числовая прямая, или периодически повторяющееся бесконечное с обеих сторон множество числовых промежутков.
Функция у = f(x) возрастает (убывает) на некотором промежутке, если для любых двух значений аргумента x из этого промежутка большему значен и юл: соответствует большее (меньшее) значение у.
Например, функция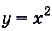 
на промежутке 
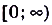; возрастает, а на 
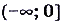убывает. Функция 
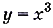возрастает на всей области определения R.
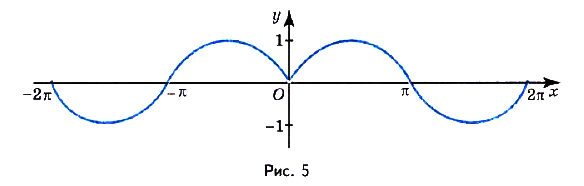
Опишем для примера свойства функции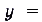 
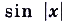
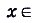
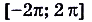, график которой представлен на (рис 5).
- Область определения
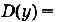
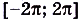. - Область значений Е(у) = [-1; 1].
- Функция чётная.
- Функция не периодическая.
- График функции с осью Оу пересекается в точке (0; 0).
- Функция имеет пять нулей:
, 
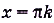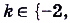
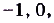
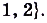
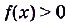, если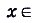 
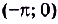
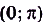;- f(x) < 0, если
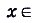
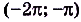
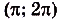. - Функция убывает, если
, 
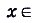
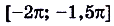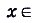
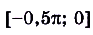и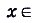 
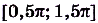
- функция возрастает, если
,
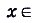
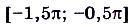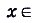
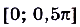и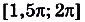 
. - Функция имеет наибольшее значение у = 1, если х = ± 0,5 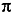и наименьшее значение у = -1, если х = ± 1,5.
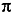Исследовать функцию можно и без построения графика — с помощью формулы, которая её задаёт, и специальных методов математического анализа. С такими методами исследования функций вы ознакомитесь в следующих разделах.
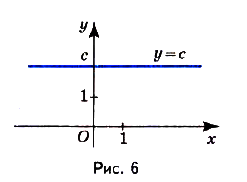
Функция у = f(x) называется рациональной, если f(x) — рациональное выражение относительно переменной х. Таковыми, в частности, есть линейные, квадратичные и степенные функции с целыми показателями. Из всех рациональных функций только функция у = с может быть периодической (рис. 6).Функция задана формулой у = 0 (на области, симметричной относительно нуля) — одновременно чётная и нечётная.
Примеры с решением
Пример №1
Для функции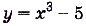 
найдите:
а) значение функции, если значение аргумента равно 10;
б) значение аргумента, при котором значение функции равно 120.
Решение:
а) Если х = 10, то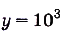 
;
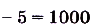
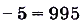б) если у = 120, то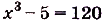 
, отсюд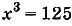а 
, а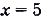 
.
Пример №2
Докажите, что функция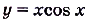 
— нечётная.
Решение:
Область определения функции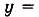 
—множество всех действительных чисел R — симметричное относительно начала координат. Найдём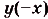 
учитывая, что у = х — нечётная функция, а у = cos х — чётная функция. Имеем: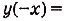
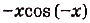
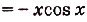
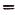
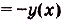. Итак, функция 
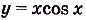— нечётная.
Пример №3
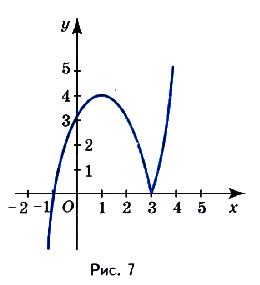
Постройте график функции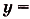 
.
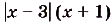Решение:
Раскроем модуль в формуле, задающей функцию:
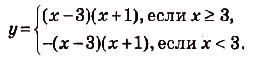
Графиком функции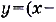 
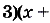
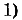, если 
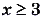, является часть параболы, которая проходит через точки (-1; 0), (3; 0) и имеет вершину в точке (1;-4). Если 
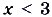, то графиком функции является часть параболы, которая проходит через точки (-1; 0), (3; 0) и имеет вершину в точке (1; 4). Графиком данной функции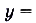 
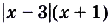является объединение обоих графиков (рис. 7).
Эта лекция взята с главной страницы на которой находится курс лекций с теорией и примерами решения по всем разделам высшей математики:
Другие лекции по высшей математике, возможно вам пригодятся:
| Предел последовательности |
| Степени с действительными показателями |
| Первообразная и интеграл |
| Показательные функции |
