Оглавление:
Формы записи комплексных чисел
Запись числа 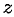 в виде
в виде 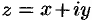 называют алгебраической формой комплексного числа.
называют алгебраической формой комплексного числа.
Модуль 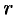 и аргумент
и аргумент 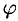 комплексного числа можно рассматривать как полярные координаты вектора
комплексного числа можно рассматривать как полярные координаты вектора 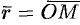 , изображающего комплексное число
, изображающего комплексное число 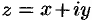 (см. рис. 161). Тогда получаем
(см. рис. 161). Тогда получаем 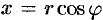 ,
, 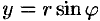 . Следовательно, комплексное число
. Следовательно, комплексное число 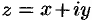 можно записать в виде
можно записать в виде 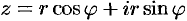 или
или
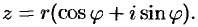
Такая запись комплексного числа называется тригонометрической формой.
Модуль 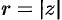 однозначно определяется по формуле
однозначно определяется по формуле
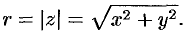
Например, 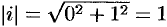 . Аргумент
. Аргумент 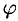 определяется из формул
определяется из формул
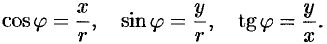
Так как
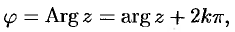
то
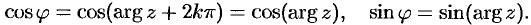
Поэтому при переходе от алгебраической формы комплексного числа к тригонометрической достаточно определить лишь главное значение аргумента комплексного числа 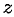 , т. е. считать
, т. е. считать 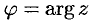 .
.
Так как 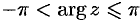 , то из формулы
, то из формулы 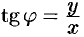 получаем, что
получаем, что
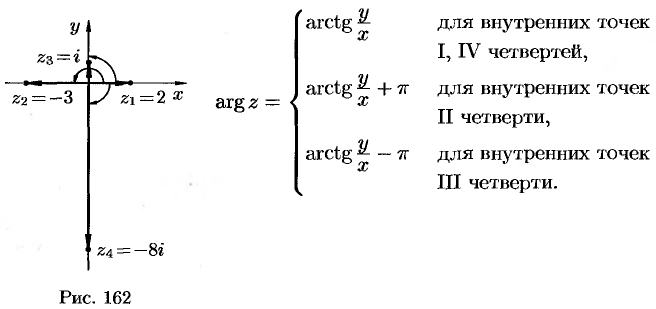
Если точка 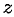 лежит на действительной или мнимой оси, то
лежит на действительной или мнимой оси, то 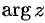 можно найти непосредственно (см. рис. 162). Например,
можно найти непосредственно (см. рис. 162). Например, 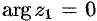 для
для 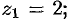
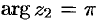 для
для 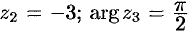 для
для 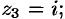 и
и 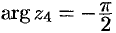 для
для 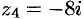 .
.
Используя формулу Эйлера
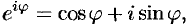
комплексное число 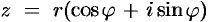 можно записать в так называемой показательной (или экспоненциальной) форме
можно записать в так называемой показательной (или экспоненциальной) форме 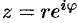 , где
, где 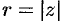 — модуль комплексного числа, а угол
— модуль комплексного числа, а угол 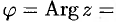
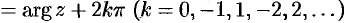 .
.
В силу формулы Эйлера, функция 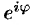 периодическая с основным периодом
периодическая с основным периодом 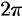 . Для записи комплексного числа
. Для записи комплексного числа 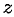 в показательной форме, достаточно найти главное значение аргумента комплексного числа, т. е. считать
в показательной форме, достаточно найти главное значение аргумента комплексного числа, т. е. считать 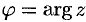 .
.
Пример №27.1.
Записать комплексные числа  и
и 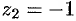 в тригонометрической и показательной формах.
в тригонометрической и показательной формах.
Решение:
Для 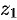 имеем
имеем
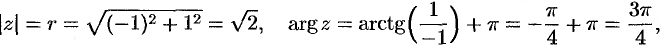
т. е. 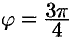 . Поэтому
. Поэтому
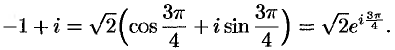
Для 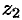 имеем
имеем
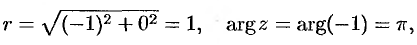
т.e.  . Поэтому
. Поэтому 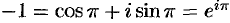 .
.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Формула Тейлора для произвольной функции |
| Геометрическое изображение комплексных чисел |
| Действия над комплексными числами |
| Свойства неопределенного интеграла |

