Применение формулы сокращённого умножения

Применение формулы сокращённого умножения

Как отмечалось выше, формулы сокращённого умножения нередко используются во время преобразований с целью упрощения решения задачи. Приведём пример.

Пример №402.

Решить уравнение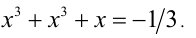

Решение:

Умножим обе части уравнения на 3 и перенесём все слагаемые в одну сторону

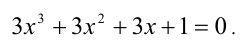
Перепишем уравнение в виде

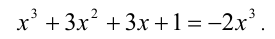
Преобразуем выражение в левой части уравнения по формуле куба суммы:

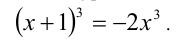
Приведя уравнение к виду 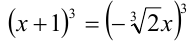, и извлекая кубический корень, получим линейное уравнение, равносильное исходному

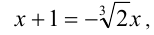
решая которое, находим единственный действительный корень

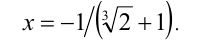
Эта лекция взята со страницы, где размещён подробный курс лекций по предмету математика:

Предмет математика

Эти страницы возможно вам будут полезны:

Уравнения вида f(x)=f-1(x), где f(x)=f-1(x)- взаимно обратные возрастающие функции

Геометрический подход при решении уравнений

Выделение полного квадрата (куба) для решения уравнений и неравенств

Рассмотрение уравнения относительного некоторой величины