Оглавление:
Формулы для вычисления моментов силы относительно координатных осей
Момент силы 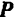 относительно какой-либо точки
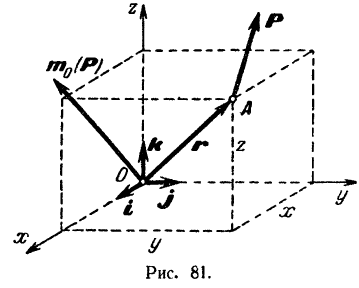
относительно какой-либо точки 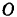 (рис. 81) может быть выражен (стр. 68) в виде векторного произведения
(рис. 81) может быть выражен (стр. 68) в виде векторного произведения
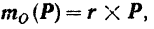
где  — радиус-вектор точки
— радиус-вектор точки 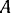 приложения силы
приложения силы 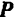 относительно точки
относительно точки 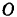 .
.
Примем точку 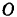 за начало системы координат и отложим на координатных осях орты
за начало системы координат и отложим на координатных осях орты 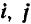 и
и 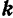 . Вспоминая, что проекция момента силы относительно точки на любую ось, проходящую через эту точку, равна моменту данной силы относительно этой оси (стр. 108), и формулу (6) разложения вектора по осям координат, можно записать:
. Вспоминая, что проекция момента силы относительно точки на любую ось, проходящую через эту точку, равна моменту данной силы относительно этой оси (стр. 108), и формулу (6) разложения вектора по осям координат, можно записать:
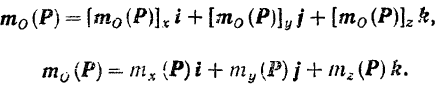
С другой стороны, из векторной алгебры известно, что векторное произведение  может быть записано в виде определителя третьего порядка
может быть записано в виде определителя третьего порядка
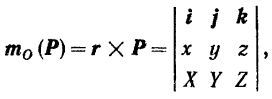
где 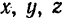 — координаты точки
— координаты точки 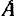 приложения силы (см. рис. 81),
приложения силы (см. рис. 81), 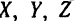 — проекции силы
— проекции силы 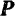 на оси координат.
на оси координат.
Раскладывая определитель третьего порядка по элементам его первой строки, будем иметь:
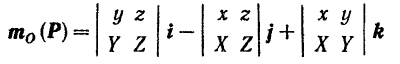
или, меняя на противоположный знак перед вторым членом правой части последнего равенства,
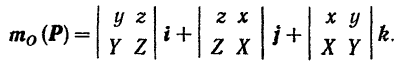
Сравнивая равенства (I) и (II), находим:
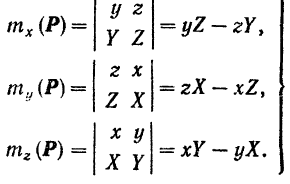
Для получения правильных значений моментов силы относительно координатных осей, при вычислении их по формулам (35), нужно подставлять в эти формулы проекции 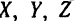 силы на координатные оси и координаты
силы на координатные оси и координаты 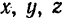 точки приложения силы с соответствующими знаками этих величин.
точки приложения силы с соответствующими знаками этих величин.
Формулы (35) нетрудно запомнить, если обратить внимание на их структуру. Момент силы относительно какой-либо координатной оси выражается определителем второго порядка, в первой строке которого стоят координаты точки приложения силы, во второй — проекции силы на оси, соответствующие тем же координатам. Координаты точки приложения силы записываются в порядке обхода осей координат против часовой стрелки. Если вычисляется момент силы относительно оси 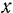 , то в первой строке определителя записываются координаты
, то в первой строке определителя записываются координаты 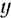 и
и 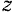 . Если относительно оси
. Если относительно оси 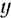 , то записываются координаты
, то записываются координаты 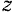 и
и 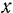 . Если относительно оси
. Если относительно оси 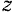 , то записываются координаты
, то записываются координаты 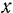 и
и 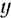 .
.
Пример задачи:
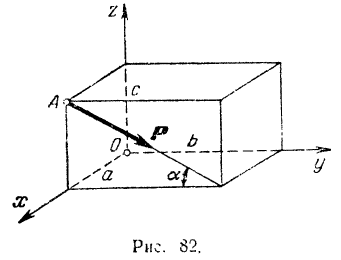
Вычислить моменты силы 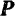 относительно координатных осей
относительно координатных осей 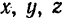 . Сила
. Сила 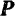 направлена из точки
направлена из точки 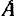 по диагонали боковой грани прямоугольного параллелепипеда (рис. 82), длины ребер которого
по диагонали боковой грани прямоугольного параллелепипеда (рис. 82), длины ребер которого 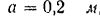
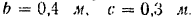 . Модуль силы
. Модуль силы
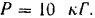
Решение:
Как видно из рис. 82, .точка 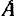 приложения силы определяется координатами:
приложения силы определяется координатами:
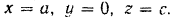
Проекции силы на оси координат:
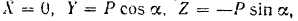
где
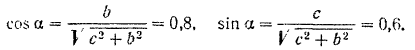
Воспользовавшись для вычисления моментов силы относительно осей координат формулами (35), будем иметь:
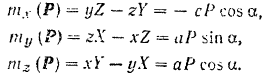
Подставляя числовые данные, получаем:
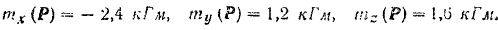
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

