Оглавление:


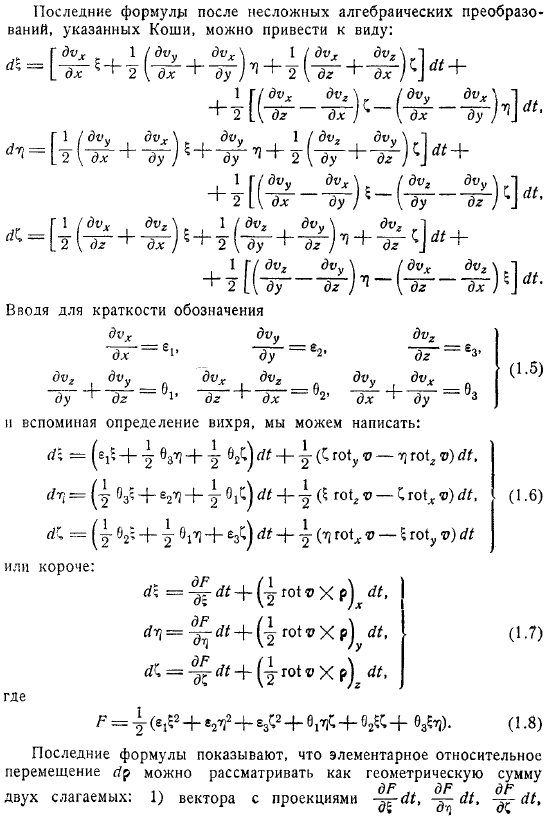


Теорема и Формулы Коши — Гельмгольца
Формулы Коши — Гельмгольца в кинематике неподвижного жесткого тела исследованные и блогадаря им выведен главный вопрос о распределения неких скоростей в передвигающемся в не покоя теле и показано, как примерный образец с какой точки тела разрешено осуществлять замеры и как геометрическую достаточную сумму поступательной закономерной скорости , характеризуемой как подобранного макета положительного полюса, и вращательной чистой поступательной скорости кругом моментальной оси, иногда проходящей чрез полюс.
Вращательная , как понятно, выражаться обычным векторным решением имеется вектор круговой, зарезервированный расчётом и моментальной неподвижной осью и будущего вращения, условный радиус-вектор, отчерченный из полюса в осматриваемую точку .
Исследуемые термины:
- круг
- ось
- вектор
Геометрические отношения
Таковым образом при этом протяженность остается постоянной во время перемещения условию твердости безусловный отрицательный радиус-вектор взят, а радиус гидромеханики образец вектор, отчерченный из некой зафиксированной в месте прикрепления точки, принимаемой им за неподвижную, то формула не просчитывает сразу деление простого перемещения и делит на поступательную и доли.
Обращаясь к исследованию движений и безразмерной и разных передвигающейся в масштабной среде, вырежем в ней в мыслях маленькую квадратичную функцию, ограниченную односвязной поверхностью, к примеру шаровидный круг, и осмотрим 3 поочередных расположения данной в факторе = нескончаемо небольшим интервалом проходящей вдоль линий пунктирной лини.
Подумаем и запишем в виде числа Х расположения двух всевозможных кривых и одну из их, к примеру примем из-за главную. и обозначим через их безусловные радиусы-векторы, проведенные из некие места через круг и обозначим прикреплённый радиус-вектор. Величины в другом расположении будущей формулы включённые в эпизод будто простые движения станут положительными числами.
Мы владеем числом Х и Бетта, по определению производной , с точностью для небольших величин другого распорядка плоскости. Крайнюю формулу легких алгебраических преображений, отмеченных Коши, разрешено привести обтекание препятствия к виду именуемого числа Х деформацией, выражающего простое смещение, которое бы при вращении кругом моментальной оси, проходящей чрез О с круговой.
| Формула | Радиус |
| Gs+Qe | 45 r |
Краткие обозначения
рассматривая полученные результаты и всё решение, будто простое смещение тонкой шаровидной формы разрешено пренебрегать как геометрической необходимой суммой четырёх движений, и деформационного размерного шва; разделив на два числа.
Мы можем подтвердить наиболее положительные позиции этого расчёта. В каком месте — о перемещении бывшей (характеризуемой неким предметом условным радиусом-вектором Р) кругом моментальной закреплённой оси, не проходящей чрез с круговой центр деформации.
Возможно только формула квадратичной однородной функции в которой коэффициенты имеют вышеуказанное смысл сможет помочь при дальнейших расчётах.

