Идея метода трапеций похожа на идею метода прямоугольников: попытаться заменить исходную криволинейную трапецию ступенчатой фигурой, состоящей из трапеций. Для этого
выполним следующие действия (рис. 47.3).
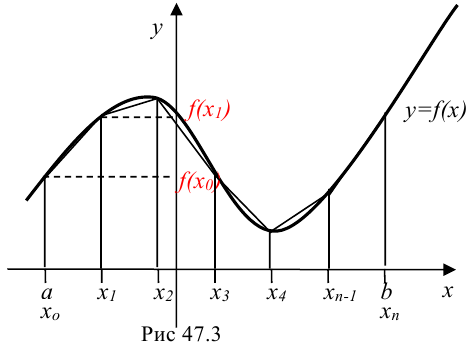
1. С помощью точек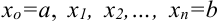 
разобьём отрезок 
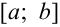на 
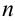равных частей длиной 
.
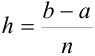2. На каждом отрезке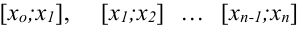 
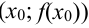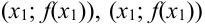построим трапеции, соединив отрезками точки 
и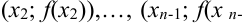 
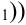и (
и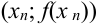 
.
3. Найдем площадь каждой трапеции как произведение полусуммы её оснований на высоту. Длины оснований первой трапеции будут равны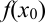 
и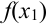 
, а высота 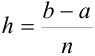. Тогда
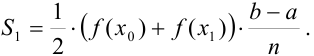
Для второй трапеции длины оснований равны 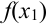и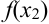 
, а высота та же: 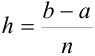. Тогда
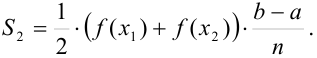
Аналогично
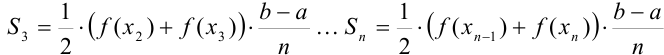
Найдем сумму площадей всех трапеций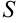 
: 
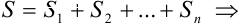
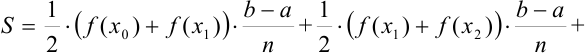
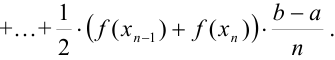
Вынесем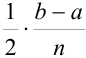 
за скобки:
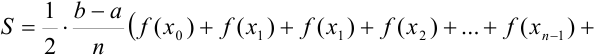
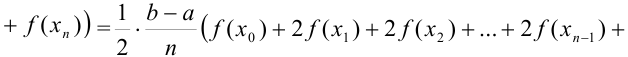
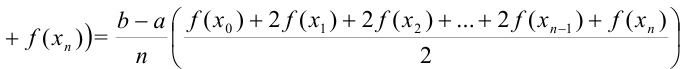
или
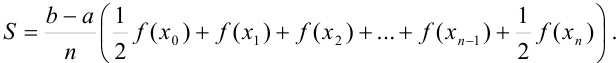
Поскольку сумма площадей всех трапеций 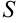приближенно равна площади криволинейной трапеции, то можно считать, что
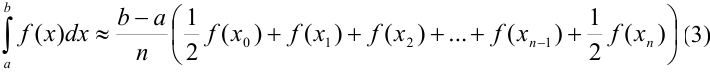
— формула трапеций.
Пример №47.2.
Вычислите приближенное значение определенного интеграла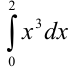 
по формуле трапеций (число точек деления 
).
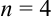Решение:
Воспользуемся решением примера 47.1. Рассмотрим функцию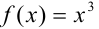 
на отрезке [0; 2], который разбит на четыре части шириной 
.
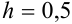В уже созданной в Microsoft Excel таблице в ячейку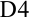 
запишем формулу для расчета приближенного значения определенного интеграла 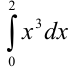по формуле трапеций (3).
Поскольку шаг равен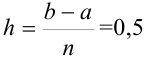 
, то его нужно умножить на скобку, содержащую полусумму первого и последнего значения функции и сумму всех остальных значений функции из столбца 
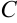. Тогда формула в ячейке 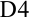будет иметь вид: 
.
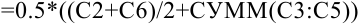Расчетная таблица будет следующей:
Полученное по формуле трапеций значение определённого интеграла (4,25) ближе к реальному значению (4), чем значения, вычисленные по формулам прямоугольников. Рассмотрим последний метод — метод парабол — и оценим его точность.
