Оглавление:
Формула Тейлора для произвольной функции
Рассмотрим функцию  . Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию
. Формула Тейлора позволяет, при определенных условиях, приближенно представить функцию  в виде многочлена и дать оценку погрешности этого приближения.
в виде многочлена и дать оценку погрешности этого приближения.
Теорема 26.1. Если функция  определена в некоторой окрестности точки
определена в некоторой окрестности точки  и имеет в ней производные до (
и имеет в ней производные до ( + 1)-го порядка включительно, то для любого
+ 1)-го порядка включительно, то для любого  из этой окрестности найдется точка
из этой окрестности найдется точка 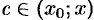 такая, что справедлива формула
такая, что справедлива формула
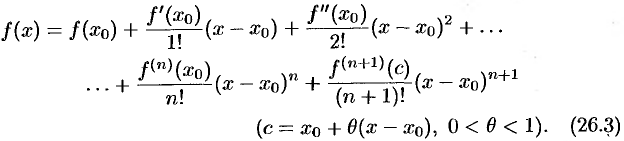
Формула (26.3) называется формулой Тейлора для функции  . Эту формулу можно записать в виде
. Эту формулу можно записать в виде 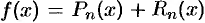 , где
, где
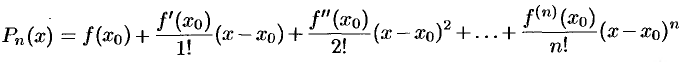
называется многочленом Тейлора, а
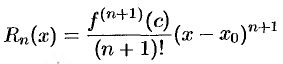
называется остаточным членом формулы Тейлора, записанным в форме Лагранжа. 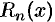 есть погрешность приближенного равенства
есть погрешность приближенного равенства 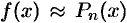 . Таким образом, формула Тейлора дает возможность заменить функцию
. Таким образом, формула Тейлора дает возможность заменить функцию  многочленом
многочленом 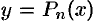 с соответствующей степенью точности, равной значению остаточного члена
с соответствующей степенью точности, равной значению остаточного члена 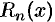 .
.
При 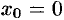 получаем частный случай формулы Тейлора — формулу Маклорена:
получаем частный случай формулы Тейлора — формулу Маклорена:
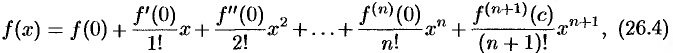
где 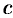 находится между 0 и
находится между 0 и 
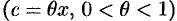 .
.
При 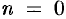 формула Тейлора (26.3) имеет вид
формула Тейлора (26.3) имеет вид 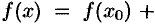
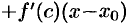 или
или 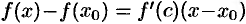 , т. е. совпадаете формулой Лагранжа конечных приращений. Рассмотренная ранее формула для приближенных вычислений
, т. е. совпадаете формулой Лагранжа конечных приращений. Рассмотренная ранее формула для приближенных вычислений 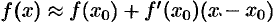 (см. «дифференциал функции») является частным случаем более точной формулы
(см. «дифференциал функции») является частным случаем более точной формулы
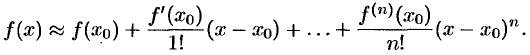
Пример №26.2.
Найти число 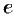 с точностью до 0,001.
с точностью до 0,001.
Решение:
Запишем формулу Маклорена для функции 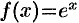 . Находим производные этой функции:
. Находим производные этой функции: 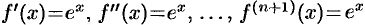 . Так как
. Так как 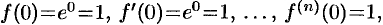
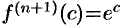 , то по формуле (26.4) имеем:
, то по формуле (26.4) имеем:
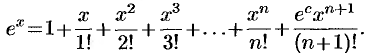
Положим 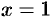 :
:
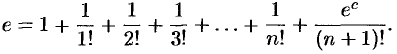
Для нахождения 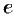 с точностью 0,001 определим
с точностью 0,001 определим  из условия, что остаточный член
из условия, что остаточный член 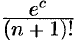 меньше 0,001. Так как
меньше 0,001. Так как 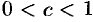 , то
, то 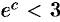 . Поэтому при
. Поэтому при 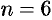 имеем
имеем
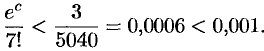
Итак, получаем приближенное равенство
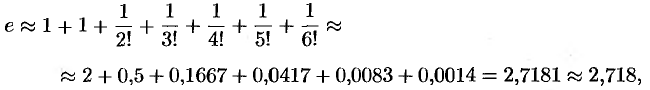
т.е. 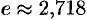 .
.
Приведем разложения по формуле Маклорена некоторых других элементарных функций:
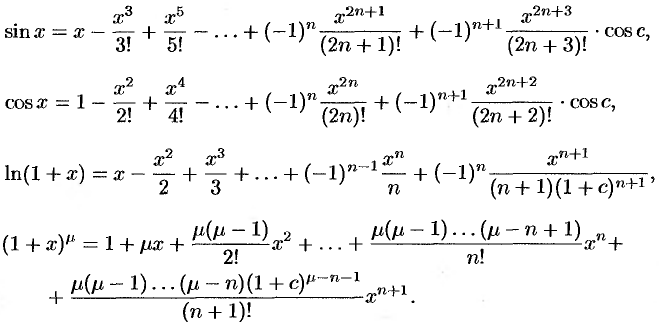
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Формула Тейлора для функции |
| Формула Тейлора для многочлена |
| Геометрическое изображение комплексных чисел |
| Формы записи комплексных чисел |

