Формула Тейлора
В определении функции  не говорится о том, при помощи каких средств находятся значения у по значениям
не говорится о том, при помощи каких средств находятся значения у по значениям  . В тех случаях, когда функция является формулой вида
. В тех случаях, когда функция является формулой вида 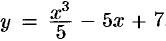 , значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций
, значения функции найти легко с помощью четырех арифметических действий. Но как найти значения, например, функций 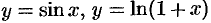 при любых (допустимых) значениях аргумента?
при любых (допустимых) значениях аргумента?
Для того, чтобы вычислить значения данной функции  , ее заменяют многочленом
, ее заменяют многочленом 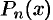 степени
степени  , значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
, значения которого всегда и легко вычисляемы. Обоснование возможности представлять функцию многочленом дает формула Тейлора.
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
| Правило Лопиталя и раскрытие неопределённостей |
| Раскрытие неопределенностей различных видов |
| Формула Тейлора для многочлена |
| Формула Тейлора для произвольной функции |

