Оглавление:


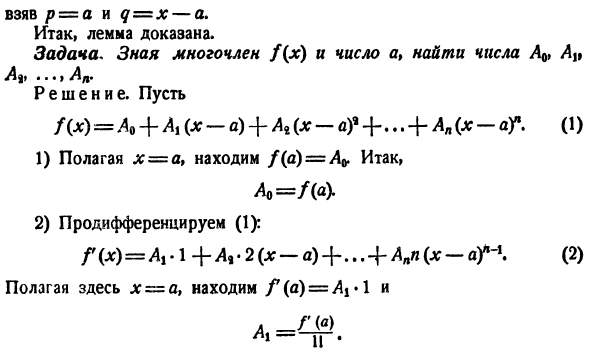







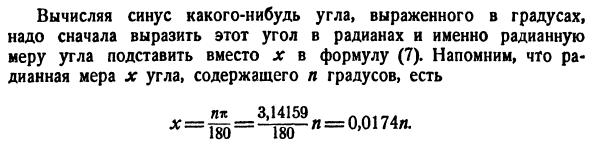




Формула Тейлора
- Тейлор официальный Н°1.Постановка вопроса. Напомним определение функции, данное в разделе II:. если каждому значению x соответствует определенное значение^*, то переменная y является функцией переменной X. Это определение абсолютно не упоминает о средствах нахождения значения y, соответствующего значению
данного x. Если у вас есть формула, подобная формуле Проблема очевидна. Однако это не относится к более сложным случаям. у = Sin х Не тот, кто знает только школьные курсы тригонометрии、 Это формула. То же самое относится и к равенству. г = brctgx, г ==] Вышеизложенное приводит к важной задаче создания инструмента анализа, который может найти
у = Х * «Ли х * — 4hya + 3х-7 Г = — Ф + Б-• Людмила Фирмаль
значение функции по значениям ее аргументов. Формула Тейлора, представленная в этом разделе, является одним из возможных решений этой проблемы. н°2.Уравнение теблура многочленов. Лемма. F(х)= ЦБ + СЈ, х — {- с ^ х * + … + СиДжей? Некоторые полиномы. Каким бы ни было число, наш многочлен можно записать
в следующем виде + … + (Х-аг、 Где A, Av Av Ap-некоторая константа. Доказательство. Многочлен f (x) — это сумма степеней jc\, умноженная на константу c*.Поэтому достаточно убедиться, что можно записать еще одну степень xk в виде суммы. х * = АВ — \ — Ах(х-а)+ Aiix-… + Ак (х-оф. Однако последнее очень очевидно, потому что x можно описать как сумму. применение бинома Ньютона при х = АА)
- и (р + ч?= / + В -’?+ + … +(?、 возьмем p = a и q = x-a. следовательно, Лемма докажет. Спросил. Зная многочлен f (x) и число a, находим число A0> A»i4j»•. * » ? Решение. Позвольте мне. Ф(Х)= АО + в(Х-а)+ АИ(х-ДФ + … + (Х-ар.(1) 1) если x = a, то F (a)= A *найдено. А0 =нет 2)
дифференциация (1): +Анти{х-а?- (2) Если вы поставите здесь x = a, вы найдете (a)=Л1•1. 3) дифференциация (2): / * ( * ) = 88.2.14-гг3.2 (ГГ-a)+… + An (n-1) (—a) n *и поставим здесь x = a, тогда f ’(a)= * 1.2 и Ла-2.И если мы продолжим это рассуждение、 И вообще _ / <«>(ля) Таким образом, для любого многочлена f (x) и любого числа a выражение Это называется Taylor official*). Образцы. скажем Ф (Х)= Х? — 3 раза *- \ —
— 3х+ 4х-8, Ф(2)= −4,р(х)= B* *-6 * -Ф4, Ф(2)= 4,Ф не *) Людмила Фирмаль
4х-8. разверните f (x) с силой x (2).Решение. F(х)= * * = 6х-6,Ф *(2)= 6 /> «()= 6、/«(2)= 6、 И так оно и есть.、 lg3-zdr9 4lg-8 = −4 + 4 (d:-2)+ 3 (jc-2) ’-{-(-2f. П°3.Формула Тейлора для любой функции. пусть f (x) — любой континуум функций и имеет непрерывные производные всех порядков. Выберите И Л и создать полинома Т (х)= «да») -«)+… + ^-(х-АФ、
Мы называем это полиномом Тейлора функции f (x). потому что мы не предполагаем, что F (X) является полиномом**)、 * ) В. Тайло’Р (1685-1731) — английский математик. * * ) Под многочленами (иногда алгебраическими а и многочленами), как упоминалось выше, понимается функция вида:+ + f (x) — T (x. и больше ничего не могу
сказать. Однако есть очень много случаев, когда разница между f (x) и T (x) оказывается очень маленькой. Как правило, точность приближенного уравнения РХ) Д * т(х) Так как T (x) является нормальным алгебраическим многочленом, и его вычисления не вызывают проблем, выражение f (x) g T (x) является функцией f(x \ Чтобы оценить ошибку равенства f (x)^ T (x), нам нужно вывести
удобную формулу для разности /()- г(4 В общем, расчет вполне laborious. To упростим задачу, если η= 2, то есть многочлен Тейлора равен Т(Х)= ф (<2)+ ф (А) (х-а) (х-) Решение интересующей нас задачи осуществляется с помощью следующей искусственной методики). фиксируя x и заменяя константу a переменной t, мы вводим функцию
или (x-ay-J W 31 3!) Таким образом, используя выражение T (x), выражение (4 )) Для простоты будем считать, что N = 2.В общем случае, формула X находится между ними. Это называется формулой Тейлора, которая имеет модульный член в виде Лагранжиана. Этот
остаточный членявляется последним членом или выражением справа от(5). L + 1 (6) Я не знаю его точное значение, потому что я не получаю точку X.Однако во многих случаях можно оценить термин RH (x), который устанавливает нечто, не превышающее абсолютного значения этого термина. Если окажется, что остаточный срок невелик, то от него. Если вы их проигнорируете,
то получите приблизительную формулу Образцы. 1. Примените формулу Тейлора к функции/(jc)= sinng и используйте) a-0 и η= 8. Ф(Х)= Sin х、 /(JC)=: C0SJC、 F ’(х)= — Sin х、 ДМ (х)= — соѕ х,/(>(йк) = грех *、 •「• о••• Поэтому, если вы представляете точку между 0 и q с помощью X, это выглядит так: грех. и-и| ** * 7 1 cos ^ o ssn X-X s, — f 51 71 * 91 Если вы проигнорируете оставшийся член, вы получите приближенное уравнение /(0)-0、/ 00)= b / 40)= o, гамма(0)=-1, f <4) (0)= 0、 (7 ))
потому что х 91.я9, его абсолютное значение Это ошибка равенства Например, вычислить по последнему выражению Максимально. Девяносто один Грех, мы совершаем ошибки. 2″. Девяносто один < у-8. При вычислении знака определенного угла, выраженного в градусах, необходимо сначала представить этот угол в радианах, а вместо
x в формуле (7) подставить радианы углов. радиальное измерение угла, содержащего N градусов х Л * 3.14159 LL17. Х = = Т = — 1ж-Н = = t74n ’ 2) применить формулу Тейлора к функции f (x)= e >и взять a = 0 и n = 7. Потому что для каждого k существует/ lA) (x)= ex, f(k) (0)= 1 и -. Х Y х*. х *, ХК, х%, Х9, Х1. е * о е= 1 +П+2Г+Ж+4Г+5Г+В| + 7Т + 8Т ^в
частности, Х = 1, то остаток отбрасывается, когда вы、 + ^ + Ф + Ф + + + (8) Источник В этом равенстве есть ошибка. Но 0 e * e <3, так что ошибка 3 3 Равенство(8) положительно, меньше, чем = Щ20<С0. 00008. (8) при записи десятичной дроби в десятичные, и удерживайте десятичных б、 ^-= 0.500000 1 = 0.166667 1 = 0.041667 Сорок один 1 = 0,008333 секунды 1 = 0.001389 1 = 0.000198 0.718254 Отсюда,
с точностью 0.0001, вы получите следующее: е = 2.7183. в N°4.Другие формы формулы Тейлора. Заменить формулой * на l: — j-Ajc, а на X. получаем / С* +Дх) = / ( * ) + ЦР-ДЛГ+… если вы переместите f (x) влево и сфокусируетесь на/(jc-J-Ax) — / ( * ) = A /(x)、 (a. tj 4 — — ^ i — (уже) г ’+(я + 1)1 1′ 1!* !< А * Я»4-З_ Ln (9 )) К+ Это выражение дает расширение
& F (x) в степени Al. Если Ax-минимум 1, то погрешность уравнения А /(Х)= ф ’(*) В * Существует квадратичная бесконечно малых и эквациональной ошибка А / C) = / ’() (М * Есть бесконечные 3 следующие. Я помню работу. Нажмите здесь, чтобы узнать больше)* Представляет собой производную от N-dkf (x).Вы можете написать формулу Тейлора (9). БФ(х) — ДФ (х) — п-2И-Р-1-п — ^ ТС + ТФ ’
Смотрите также:
| Исследование функций | Касательная и нормаль |
| Основные теоремы дифференциального исчисления | Направление вогнутости кривой |

