Формула Тэта и Томсона

Формула Тэта и Томсона

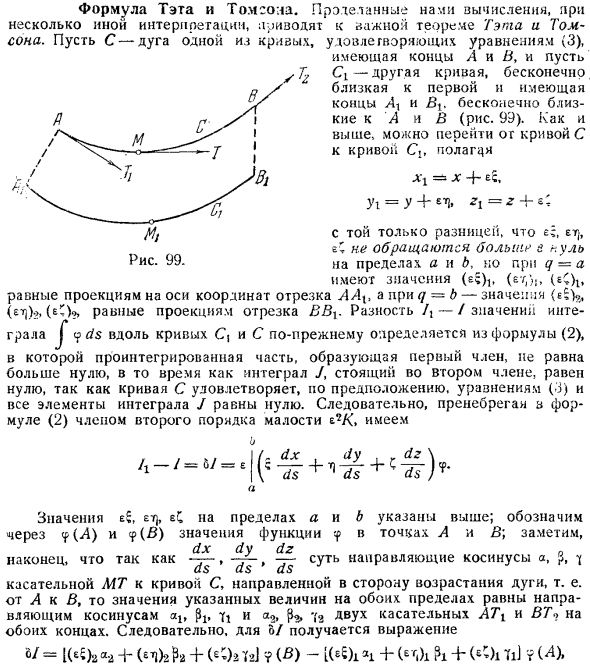
• Наши расчеты приводят к важным теоремам Тэта и Томсона, с несколько различными интерпретациями. Из кривой Пойти спать. Пусть c 1 дуга. Заполните уравнение 3, имейте концы A и B, и пусть Cl другая кривая, которая бесконечно близка к первой кривой, и конец A и Bv бесконечно к A и B рис. 99. В приведенном выше примере Вы можете перейти от кривой C к кривой Ci и настроить ее Л Дж = х 4 ЕС гг = г х г, Г1 = г 4 г. Хорошо.

Единственное различие, что ec, eiq, eC больше не исчезает на границах a и b, заключается в том, что для q = a значение e , et , Равное проекции на оси отрезка AA q = b значение E10 эквивалентное проекции отрезка BBX. Разница между значениями интеграла J yds вдоль кривых C и C D по прежнему определяется из уравнения 2.Поскольку кривая C удовлетворяет уравнению 3 по предположению, а все элементы интеграла J удовлетворяют следующему уравнению, то Интеграл в пункте 2 равен нулю, но s больше нуля становится нулем, поэтому мы игнорируем его в уравнении 2 как член квадратичного уравнения E2K J yds C вдоль кривой C по прежнему определяется по формуле 2. б Но…

Мы увидим дальше, что принцип возможных скоростей дает значительно более быстрый метод для решения подобных вопросов. Людмила Фирмаль

Значения e , etj и eC в a и b перечислены выше. Обозначим значения функций y в точках A и B через p A и y B .Примечание: ДХ ды dzЛо И наконец, потому что r r t r это Косинус направления a, ds ds Увеличение касательной MT к кривой C в сторону дуги, то есть от A до B, величина этих величин обоих пределов равна Косинусу направления 1 и a2 14 2 АВУХ касательных ATt и BT Итак, для o , вы получаете выражение Вт = Се5 2 А2 4 эт 2 Р2 + а 2 7 й B L например x + Искусство. , 4. , 71 Л, существует простая геометрическая интерпретация. е 2 А2 4 эт 2 е 2 Представляет собой проекцию отрезка BB на касательную VT2, которая равна BBi cos Tbbi. Аналогично, 2 я величина, содержащаяся в, равна AA cos 1 AAV.

Окончательно С ББ и B в COS Ф BBX по Л потому что 4 Баат В теории развертки Или в более симметричной форме 5 = гггг COS Лл лхухувв cos55 angle угол abbt дополняет угол t2bbx и угол равен углу txaax. Формула тета и Томсона 4 полностью аналогична известной базовой формуле, представляющей изменение длины прямого отрезка, и выведена из нее для cp i Bertrand, Differential calculus course, p.22. Результаты, полученные из уравнения 4, совпадают с результатами, полученными из аналогичных уравнений в теории прямых и параллельных кривых и поверхностей. Здесь мы покажем результаты, которые приносят интересные результаты в теорию бракистокрона. Принцип минимального действия и теория задачи преломления.

• Тогда будем считать, что функция p не исчезает в области рассматриваемого пространства. Приложение г. Учитывая 2 поверхности S и, но какую кривую мне нужно нарисовать от одной поверхности к другой, чтобы Интеграл вдоль этой кривой был максимизирован или минимизирован Пусть A и B рис. 100 2 неизвестные точки, пересекающие искомую кривую И то и другое surfaces. In в частности, эта кривая будет 1 из них. Соедините точки A и B, которые максимизируют или минимизируют интеграцию I. 

Это одна из кривых с, определяемая формулой 31 1.In чтобы определить точки A и B, измените Интеграл между 2 поверхностями на максимальную или минимальную кривую при переходе от AC B к любой почти бесконечной кривой, в частности, для другой бесконечно близкой кривой C, вариация 6 должна быть равна 0.Вычислите это изменение при переходе от кривой AC B к другой бесконечно близкой кривой C пусть кривая AEBX 34 2 с болит. Из той же точки А она заканчивается точкой Bx выше. Затем, основываясь на приведенной выше формуле Д = Б потому что ABX. Косинус должен быть равен нулю, потому что вариация 5 должна быть равна нулю.

Чтобы показать, как можно составить вспомогательные условия равновесия, рассмотрим прямоугольный стол, опирающийся четырьмя ножками на горизонтальную плоскость. Людмила Фирмаль

Поэтому угол ABBX должен быть прямым для всех положений точки Bx на поверхности 2, а искомая кривая C перпендикулярна этой поверхности. Точно так же она перпендикулярна поверхности. в частности, = = В этом случае получается известный базовый результат. Она заключается в том, что нужно нарисовать общую Нормаль на обеих поверхностях, чтобы найти кратчайшее расстояние между и S. Это указывает на то, что искомая кривая является диаграммой равновесия нити, концы которой скользят без трения по 2 поверхностям, а натяжение равно. А силовая функция равна авг. Очевидно, что если 1 из поверхностей заменяется фиксированной кривой или точкой, то применяется та же теорема. 2. Теорема тета и Томсона.

Если принять во внимание кривую C, которая представлена уравнением 3 и перпендикулярна заданной поверхности S, и на каждой из этих кривых кривая S откладывается от точки A, пересекающей поверхность S, то дуга AB является точкой пересечения двух кривых. Я м Ля Значения, взятые вдоль этой кривой, имеют одинаковые постоянные значения для всех кривых, а геометрическое положение точки B это поверхность s, перпендикулярная всем кривым. Фактически рис. 100, когда мы переходим от кривой C к кривой C, близкой к бесконечности, вариация, заданная в уравнении 4 5, становится нулевой по предположению, но поскольку cos flAA = 0, кривая C перпендикулярна S, а cos = 0, кривая C перпендикулярна S. 

Смотрите также:

Решение задач по теоретической механике

Естественные уравнения равновесия нити на поверхности	Рефракция
Исследование одного определенного интеграла. Геометрическая задача	Натяжение и изгибающий момент