Формула Симпсона

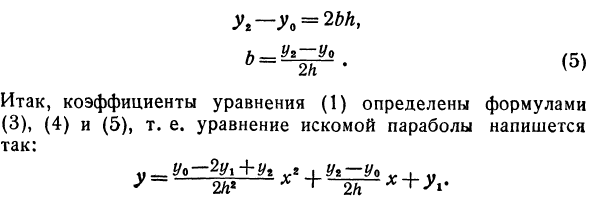
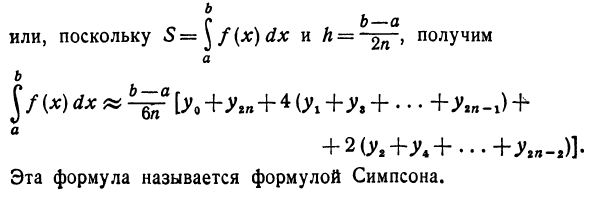
Формула Симпсона

• Помимо приблизительного вычисления интегралов с использованием интегральных сумм, существуют различные формулы, которые представляют приблизительно определенные интегралы. Мы выводим один из них, так называемое «уравнение Симпсона». Чтобы получить его, мы сначала решаем две проблемы. Задача 1. Парабола y = a>? Рассчитайте площадь изогнутой трапеции в окружении. + Bx + c, прямая x- / r, x = h и горизонтальная ось. Решения. Как было показано ранее, площадь изогнутой трапеции представлена ​​определенным интегралом.

Рассчитайте интеграл и сделайте возможные упрощения. Л ч ч S = a J xx dx + b J l; dx + s J dx = + b [t-Tg1] + c [h — (- h)] = lah ‘+ 2ch. Следовательно, желаемая площадь выражается как: S = ^ ах9 + 2ч. (1) Задача 2. Напишите параболическое уравнение через точки A (—h, y0), B (0, yy) и C (k> yy). Здесь числа y01, yt и yy являются произвольными, а h — произвольным положительным числом.

В рассматриваемом случае этот интеграл записывается как час S = $ (ax * + bx + c) dx. -h Людмила Фирмаль

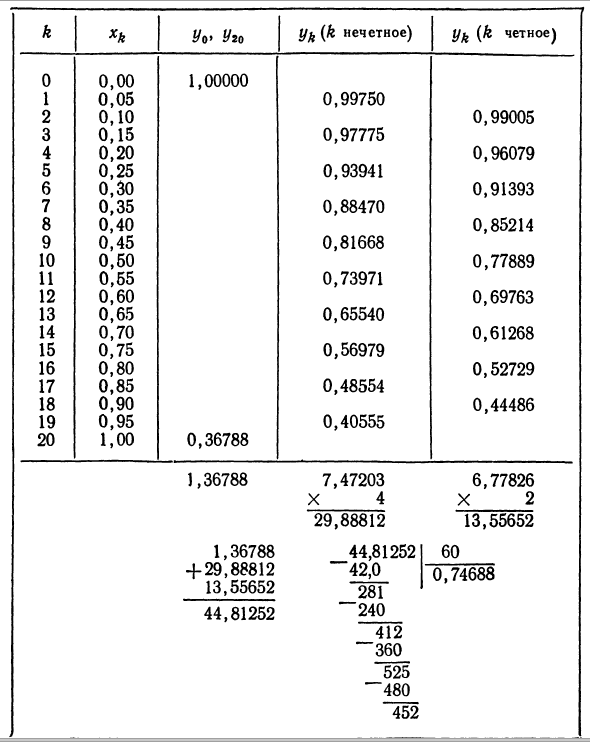
Кроме того, рассчитать площадь изогнутой трапеции,Пример 2. Интеграция ^ e ~ * 7 Снова вычислите dx. о Это было почти рассчитано в §1. Разделите интервал интегрирования на 20 частей. Напомним, что метод Симпсона требует четного количества деталей. Запишите значения подынтегральных функций и поместите их в таблицу определенным образом.

k H 00 »Y» yk (нечетное число k) yk (четное число k) 0 0,00 1,00000 1 0,05 0,99750 2 0,10 0,99900 3 0,15 0,97775 4 0,20 0,96079 5 0,25 0,93941 6 0,30 0,91393 7 0,35 0,88470 8 0,40 0,85214 9 0,45 0,81668 10 0,50 0,77889 11 0,55 0,73971 12 0,60 0,69763 13 0,65 0,65540 14 0,70 0,61268 15 0,75 0,56979 16 0,80 0,52729 17 0,85 0,48554 18 0,90 0,44486 19 0,95 0,40555 20 1,00 0,36788 1,36788 1.36788 + 29.88812 13.55652 44,81252 60 412 360 525 «» 480 7,47203 X_4 29,88812 44,81252 42,0 6,77826 X_2 13,55652 0,74688 281240 Таким образом, использование формулы Симпсона дает приближение 1 ^ е ~ х * дх «0,74688. о В результате правильные первые 3 десятичных знака (это можно сделать, сравнив число результатов с количеством приращений интервала или оценив сложные, но возможные ошибки Может быть установлен).

• По сравнению с результатами, полученными в § 1 (при делении на 20 частей), вы можете увидеть преимущества формулы Симпсона. Для того же объема работы, эта формула дала три правильных десятичных знака, но § 1 дал только один правильный знак.

Окруженный этой параболой, абсциссой и прямыми линиями x = -h и x-h. Решения. Желаемое уравнение параболы можно записать в виде: y = ax2 + bx + c. (2) По условию точка A должна находиться на параболе, поэтому ее координаты удовлетворяют уравнению (2). y0 = a (-h) * + b (-h) + c. (2 ‘) Условие, что точки B и C находятся на параболе, можно описать следующим образом. ух = а. bg + b.0 + c} (2 «) уу = ак * + чч + с. (2 дюйма) В уравнениях (2 ‘), (2 «), (2″‘) неизвестными являются a, b и c.

Найдите их, решив систему уравнений (2 ‘), (2 «), (2″‘). Из уравнения (2 «) с = год (3) Подставляя значения, найденные в выражениях (2 ‘) и (2’ «): y0 = ah2-bh + ylt yt = ah1 bh + yr Добавьте эти уравнения для каждого члена, чтобы найти a. L + L = + y.-2uh + y% 2h2 1 I * ‘ Затем вычтите первое из второго, чтобы найти b.

Следовательно, коэффициент в уравнении (1) определяется уравнениями (3), (4) и (5). +Чтобы рассчитать площадь, примените результат задачи 1 и подставьте значения c и a в уравнения (3) и (4) уравнения (1). Будет иметь Позволяет упростить: S = j (y-2y1 + yt) h — [- 2ylh = Требуемая площадь представлена формулой 5 = + (6)

Другими словами, искомое уравнение параболы записывается в виде: у- ш * т 2ч * Людмила Фирмаль

Это уравнение можно прочитать следующим образом: Площадь, ограниченная длиной параболы, двумя ординатами y0 и yt и отрезком 2L на горизонтальной оси, равна одной трети произведения двух факторов. Первый фактор представляет собой сумму полярных координат y0 и y2 и в 4 раза больше средней ординаты yv, а второй фактор равен половине длины горизонтальной оси или h. Пример 1. Вычислить площадь, ограниченную параболой y = -Xx + 6x с прямыми линиями x = \ и n; = 5 и сегментом горизонтальной оси Найти полярные координаты: y9 = -Г + 6-1 = 5, у2 = = -52 — (- 6 • 5 = 5.

Горизонтальный отрезок 2h-b — 1 = = 4, h = 2. Точка 1 + 5 Сегмент, т. Е. Абсцисса x = — = 3, поэтому средняя ордината yx = -3 * + 6-3 = 9. Используя уравнение (6) 5 = 1 (5 + 4-9 f 5) 2 = |. Применить результат к приближению б Вычисление определенного интеграла ^ f (x) dx. Это интеграл но Можно рассматривать как изогнутую область трапеции, Ограниченная кривая y = f (x), прямая x = a> x-b И горизонтальная ось. Поэтому приблизительный расчет int Грааль ^ f (x) dx эквивалентно плоскому приближению но Сделайте указанную трапецию запасной. Площадь трапеции представлена 5, затем J / (JC) дх.

Разделите сегмент (a, b) на 2n равных частей. Каждая длина Части, равные h = эти мелкие части (сегменты) Абсцисса x0 = ay xx — a + h, x2 = a + 2h} Конец в точке x2n = a + 2nh-b. Через эти точки нарисуйте ординаты точек на кривой y = f (x) и покажите их Λ = / (* o). .v, = / (* «). L = / (*)> U.» = / (. «). Он заканчивается буквами A0, Av At и A2P. Точка L0, LR L2 и A2p делятся на тройки. Первые три — это точки A0, y44, / 12, вторые — это точки A2, Ar, 2P ‘

Последние три состоят из точки А Нарисуйте параболическую дугу через точки, принадлежащие одной тройке. Получить первую дугу A ^ AXA ^ вторую дугу L2L8L4, последнюю дугу A1P_% Arn_lAgp. Наконец, рассмотрим «двойные полосы». Первый из них ограничен дугой параболы A0AXA2, ординатами y0 и y2 и горизонтальным отрезком 2h.

Вторая ограничена дугой AgAgA4, ордината y2 и y4, сегмент с горизонтальной осью 2h, …, последняя двойная полоса ограничена дугой A2n_2A2n_lA2n, ордината y2p_2 и gp, сегмент 2h на горизонтальной оси. Обозначает двойную полосу sv s2, st, …, sn. Для небольших разделов, то есть для малых h}, общая площадь двойной полосы $ g + $ g ++ + ••• + sn немного отличается от области S.

Площадь двойной полосы можно рассчитать по уравнению (6). Что получить: Площадь двойной полосы sl равна ~ iy9 + ^ yl + yt) A, площадь двойной полосы st равна \ (yt + ^ y9 + y4) hi Площадь двойной полосы sn равна ^ (ytn-t + / byxn-lJrytn) h. Следовательно, общая площадь всех двойных полос выражается как: sl + s1 + … + sn = j (y0 + 4yl + y1) + j (y1 + 4yt + yJ + … + J (Ugp-g + * Ugp-g + Ugp) или «, + *, + ••• + sn = j (Л + 4Л + Л + Л + 4Л + Л + ••• т-1 + 4 года 2P-1 Объедините все y с нечетными числами и все y с четными числами, исключая y0 и y1n.

Обратите внимание, что одновременно с Ву и Ушу каждое четное число y появляется дважды. так sl + s * +. «+ sn = j [y0 + yzn + 4 (yl + yi + ..- + ytn-l) + Для малого ч примерно + … так S 4 4 [V0 + V * n + * (Vx + V + + •• + ​​Vn-r) + + 2 (L + L + -. + L * -,)] * l £ —a Или S = ^ f (x) dx и h = но В j / (X) dx «Iy0 + 4 (l + l + .. + sir-g) + + 2СУ> + УА + … + Упп-Л Эта формула называется формулой Симпсона.

Смотрите также:

Предмет высшая математика

Длина дуги	Функции многих переменных
Вычисления при помощи интегральных сумм	Координаты в пространстве