Оглавление:
Формула Остроградского-Грина
Связь между двойным интегралом по области 
и криволинейным интегралом по границе 
этой области устанавливает формула Остроградского Грина, которая широко применяется в математическом анализе.
Пусть на плоскости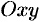 
задана область , ограниченная кривой, пересекающейся с прямыми, параллельными координатным осям не более чем в двух точках, т. е. область — правильная.
Теорема 56.2. Если функци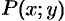и 
и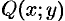 
непрерывны вместе со своими частными производным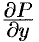и 
и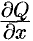 
в области , то имеет место формула
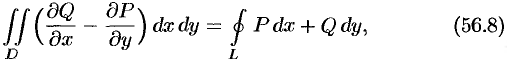
где — граница области и интегрирование вдоль кривой производится в положительном направлении (при движении вдоль кривой, область остается слева).
Формула (56.8) называется формулой Остроградского-Грина.
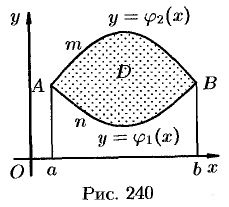
Пусть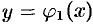 
— уравнение дуги 
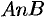, а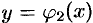 
— уравнение дуги 
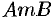(см. рис. 240). Найдем сначала 
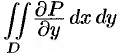. По правилу вычисления двойного интеграла, имеем:
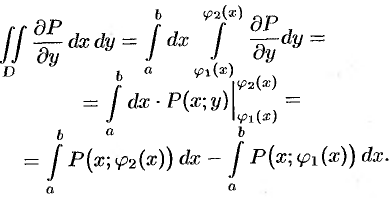
Или, согласно формуле (56.6),
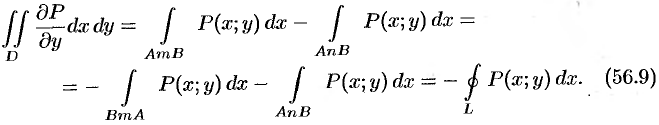
Аналогично доказывается, что
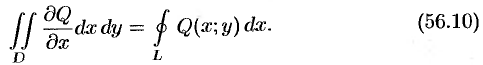
Если из равенства (56.10) вычесть равенство (56.9), то получим формулу (56.8).
Замечание. Формула (56.8) справедлива и для произвольной области, которую можно разбить на конечное число правильных областей.
Пример №56.3.
С помощью формулы Остроградского-Грина вычислить
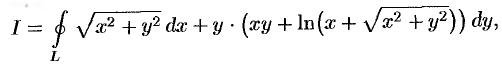
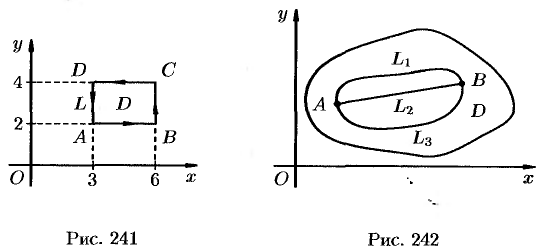
где — контур прямоугольника с вершинами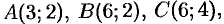 
.
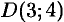Решение:
На рисунке 241 изображен контур интегрирования. Поскольку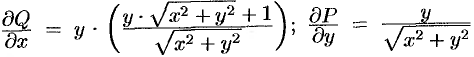 
, по формуле (56.8) имеем:
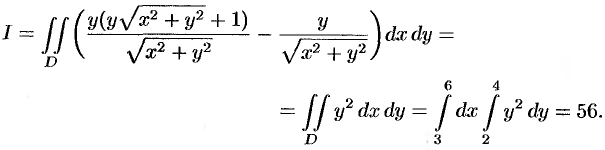
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
Другие темы по высшей математике возможно вам они будут полезны:
