Формула корней квадратного уравнения в математике с примерами решения

Оглавление:

Формула корней квадратного уравнения. Теорема о разложении квадратного трёхчлена на линейные множители

Если в квадратном уравнении (1) коэффициент b = 0 , то имеем

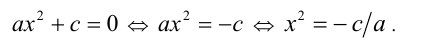
При — 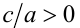Формула корней квадратного уравнения получаем корни 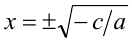, при c = 0 корень x = 0. Если же в уравнении (1) коэффициент c = 0, то имеем

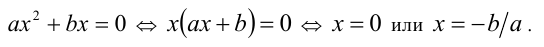
Выведем теперь формулу для корней квадратного уравнения (1) в общем случае 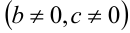Формула корней квадратного уравнения . Преобразуем левую часть уравнения, а именно вынесем коэффициент а за скобку и выделим полный квадрат:

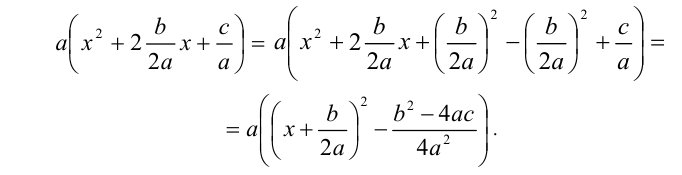
Выражение 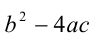Формула корней квадратного уравнения называют дискриминантом квадратного уравнения и обозначают D . Используя это обозначение, уравнение можно переписать в виде:

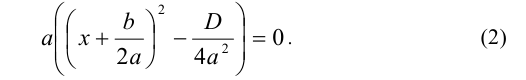
Дальнейшее решение уравнения зависит от знака D . Возможны три случая: D > 0 , D = 0 и D <0 . Рассмотрим каждый из них в отдельности.

Если D > 0 , то представим 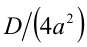Формула корней квадратного уравнения в виде 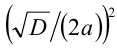, и по формуле разности квадратов получим

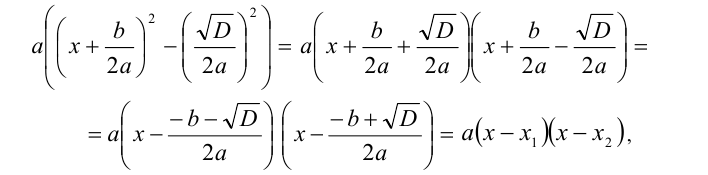
где 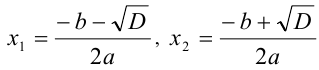Формула корней квадратного уравнения

Так как произведение двух множителей равно нулю тогда и только тогда, когда хотя бы один из множителей равен нулю (при условии, что оба множителя существуют), то можно считать доказанным, что в рассматриваемом случае квадратное уравнение имеет два различных действительных корня Формула корней квадратного уравнения и :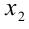

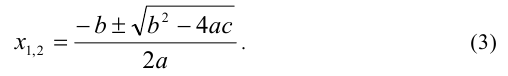
2.Если дискриминант D = 0 , то уравнение (2) принимает вид

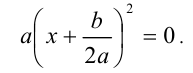
Поскольку квадрат какого-либо числа равен нулю, только если само это число равно нулю, то отсюда получаем, что уравнение имеет единственный действительный корень 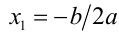Формула корней квадратного уравнения . Его можно также получить из общей формулы (3), положив в ней D = 0.

Замечание. Точнее говоря, уравнение имеет в этом случае два действительных корня, но они равны друг другу 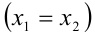Формула корней квадратного уравнения . Можно сказать также, что имеется корень , кратности 2.

3.Если же дискриминант D < 0, то — D> 0 , и в уравнении (2) во внешних скобках стоит сумма двух слагаемых

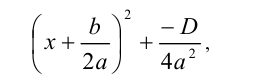
первое из которых неотрицательно, а второе — положительно. Поэтому эта сумма положительна и, следовательно, не может обращаться в нуль. Получаем, что в данном случае уравнение не имеет действительных корней. Тем самым доказана следующая теорема.

Теорема. Если 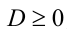, то квадратное уравнение (1) имеет действительные корни ,,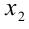 определяемые по формулам 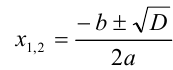, причём если 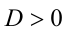, то уравнение (1) имеет два различных действительных корня 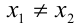; если 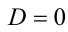, то 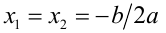— единственный корень (кратности 2); если 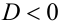, то квадратное уравнение (1) не имеет действительных корней.

Пример №154.

Сколько решений имеет уравнение

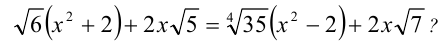
Решение:

Решим задачу стандартным способом. Чтобы оценить количество корней уравнения, вначале приведём его к стандартному виду

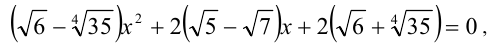
а затем вычислим дискриминант 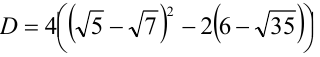Формула корней квадратного уравнения и оценим его знак, сравнив с нулем: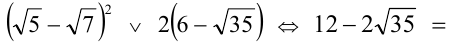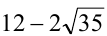. Следовательно, дискриминант равен нулю, что означает, что данное уравнение имеет единственное решение. Ответ: 1 решение.

Пример №155.

Найти все значения параметра а, при каждом из которых уравнение 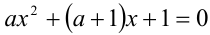имеет единственное решение.

Решение:

Для решения задачи необходимо рассмотреть два случая. Если 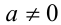Формула корней квадратного уравнения , то уравнение является квадратным, и необходимым и достаточным условием единственности решения является обращение дискриминанта в нуль, т.е.

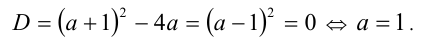
Если же 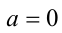Формула корней квадратного уравнения ,то уравнение становится линейным. Выясним, сколько решений оно имеет. Подставим значение 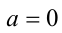в исходное уравнение, оно примет вид 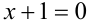Формула корней квадратного уравнения . Очевидно, что это уравнение имеет единственное решение.

Ответ: 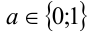Формула корней квадратного уравнения .

Попутно выше была доказана следующая теорема о разложении квадратного трёхчлена на линейные множители.

Теорема. Если квадратный трёхчлен 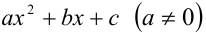имеет два различных действительных корня ,,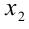 то при всех значениях переменной x справедливо тождество:

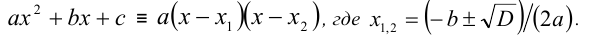
Если квадратный трёхчлен имеет лишь один действительный корень , то при всех значениях переменной x справедливо тождество

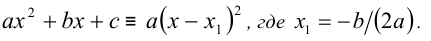
Если же квадратный трёхчлен не имеет действительных корней, то его нельзя разложить на линейные множители.

Следствие. Необходимым и достаточным условием того, чтобы квадратный трёхчлен 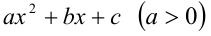Формула корней квадратного уравнения представлял собой полный квадрат, является равенство нулю его дискриминанта.

Замечание. В общем случае, если убрать в уравнении 2-й степени 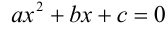Формула корней квадратного уравнения требование 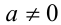, то уравнение может иметь больше двух действительных корней. Например, если 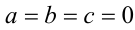, то уравнение 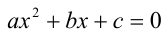имеет бесконечно много корней (любое действительное число x является в этом случае корнем уравнения).

Пример №156.

При каких значениях параметра а уравнение

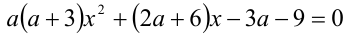
имеет более одного корня?

Решение:

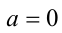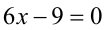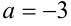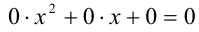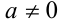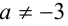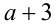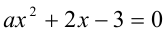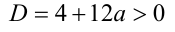
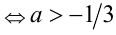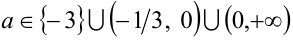Если Формула корней квадратного уравнения то получаем линейное уравнение , имеющее единственное решение. Если , то получаем уравнение вида , у которого любое действительное число x является решением. Если же Формула корней квадратного уравнения , , то, поделив на , получим квадратное уравнение , которое имеет более одного решения тогда и только тогда, когда его дискриминант положителен: Формула корней квадратного уравнения .