Формула для расчета нормальных напряжений при изгибе
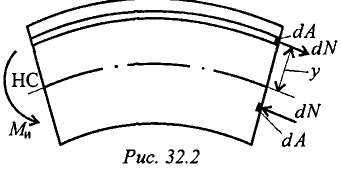
Рассмотрим изогнутый участок бруса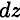 
(рис. 32.2).
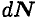— элементарная продольная сила в точке сечения;
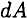— площадь элементарной площадки;
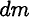— элементарный момент, образованный силой относительно нейтрального слоя.
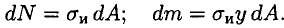
Суммарный изгибающий момент сил упругости в сечении
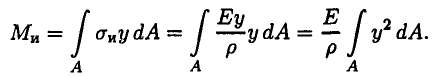
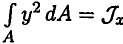— осевой момент инерции сечения (лекция 25).
Таким образом,
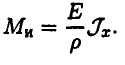
Откуда
Ранее получено
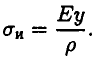
После ряда преобразований получим формулу для определения нормальных напряжений в любом слое поперечного сечения бруса:
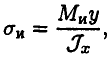
где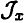 
— геометрическая характеристика сечения при изгибе.
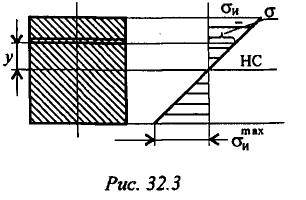
Эпюра распределения нормальных напряжений при изгибе изображена на рис. 32.3.
По эпюре распределения нормальных напряжений видно, что максимальное напряжение возникает на поверхности.
Подставим в формулу напряжения значение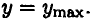 
Получим
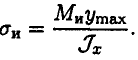
Отношение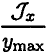 
принято обозначать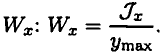 
Эта величина называется моментом сопротивления сечения
при изгибе, или осевым моментом сопротивления.
Размерность —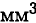 
.
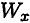характеризует влияние формы и размеров сечения на прочность при изгибе.
Напряжение на поверхности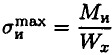 
.
Эта теория взята со страницы решения задач по предмету «техническая механика»:
Примеры решения задач технической механике
Возможно эти страницы вам будут полезны:
| Дифференциальные зависимости при прямом поперечном изгибе |
| Деформации при чистом изгибе |
| Рациональные сечения при изгибе |
| Поперечный изгиб. Внутренние силовые факторы |
