Оглавление:
Физический маятник
Физическим маятником называется любое твердое тело, имеющее неподвижную горизонтальную ось вращения, не проходящую через центр тяжести тела, и находящееся под действием только силы тяжести.
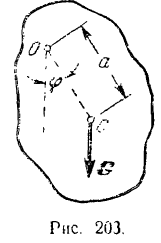
Проведем плоскость, перпендикулярную к оси вращения маятника и проходящую через центр  его тяжести (рис. 203).
его тяжести (рис. 203).
Положение маятника будет определяться углом 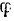 отклонения линии
отклонения линии 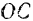 от вертикали, где
от вертикали, где 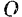 — точка пересечения оси вращения с вертикальной плоскостью.
— точка пересечения оси вращения с вертикальной плоскостью.
Обозначим через 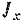 — момент инерции маятника относительно оси вращения,
— момент инерции маятника относительно оси вращения, 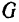 — вес маятника и
— вес маятника и 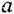 — расстояние от центра тяжести маятника до оси подвеса.
— расстояние от центра тяжести маятника до оси подвеса.
Ось вращения маятника примем за ось 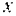 По формуле (182) можно записать:
По формуле (182) можно записать:
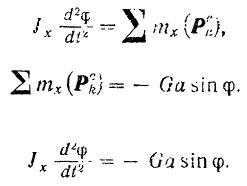
Внешними силами, действующими на маятник, будут только: сила 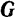 тяжести маятника и реакция
тяжести маятника и реакция 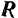 оси его подвеса. Реакция
оси его подвеса. Реакция 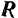 проходит через ось
проходит через ось 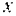 , если пренебречь трением в оси, и момента относительно этой оси не дает. Знак минус в выражении для момента силы взят потому, что знак момента силы относительно оси
, если пренебречь трением в оси, и момента относительно этой оси не дает. Знак минус в выражении для момента силы взят потому, что знак момента силы относительно оси 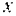 будет всегда противоположен знаку угла
будет всегда противоположен знаку угла 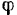 отклонения маятника (при повороте маятника против хода стрелки часов
отклонения маятника (при повороте маятника против хода стрелки часов 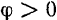 , момент силы
, момент силы 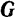 отрицателен и наоборот).
отрицателен и наоборот).
Если ограничиться только случаем малых колебаний маятника, то можно положить 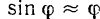 . Уравнение движения маятника принимает при этом вид:
. Уравнение движения маятника принимает при этом вид:
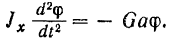
Деля обе части этого уравнения на 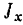 и вводя обозначения
и вводя обозначения
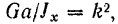
приведем уравнение малых колебаний физического маятника к виду:
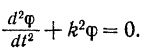
Для решения этого линейного однородного дифференциального уравнения второго порядка (с постоянными- коэффициентами) составим характеристическое уравнение
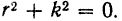
Его корни
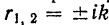
мнимые, и потому общее решение уравнения малых колебаний имеет вид:
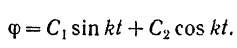
Постоянные 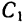 и
и 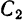 интегрирования определяем из начальных условий, полагая, что при
интегрирования определяем из начальных условий, полагая, что при 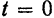 угол отклонения маятника
угол отклонения маятника 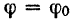 и его угловая скорость
и его угловая скорость 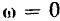 :
:
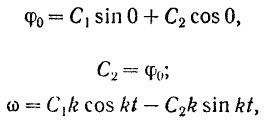
при
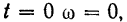
откуда
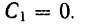
Подставляя значения постоянных 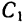 и
и 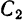 в общее решение, получаем закон малых колебаний физического маятника
в общее решение, получаем закон малых колебаний физического маятника
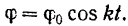
Определим период 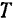 колебаний маятника, т. е. время одного его полного колебания. Круговая частота колебаний маятника
колебаний маятника, т. е. время одного его полного колебания. Круговая частота колебаний маятника
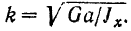
Следовательно, период 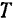 колебаний физического маятника
колебаний физического маятника
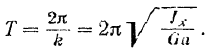
На использовании формулы (183) основан один из наиболее распространенных методов экспериментального определения моментов инерции тел.
Пример задачи:
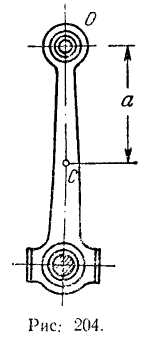
Для определения момента инерции шатуна (рис. 204) его поставили па горизонтальную призму и, отклонив на малый угол, заставили качаться вокруг горизонтальной оси. Измеренный при помощи секундомера период колебания шатуна 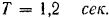 . Вес шатуна
. Вес шатуна 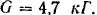 . Расстояние центра
. Расстояние центра 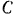 тяжести шатуна до точки
тяжести шатуна до точки 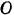 (точки пересечения оси подвеса с вертикальной плоскостью, проходящей через центр тяжести шатуна)
(точки пересечения оси подвеса с вертикальной плоскостью, проходящей через центр тяжести шатуна) 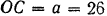 см. Определить центральный момент инерции
см. Определить центральный момент инерции 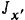 шатуна относительно оси
шатуна относительно оси 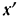 , параллельной оси
, параллельной оси 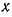 его подвеса.
его подвеса.
Решение:
По формуле (184) период колебания физического маятника (шатуна) 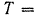
 . Отсюда момент инерции шатуна относительно оси
. Отсюда момент инерции шатуна относительно оси 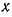 его подвеса
его подвеса 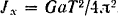 . По теореме о моментах инерции относительно параллельных осей:
. По теореме о моментах инерции относительно параллельных осей:
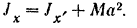
Отсюда находим искомый центральный момент инерции шатуна
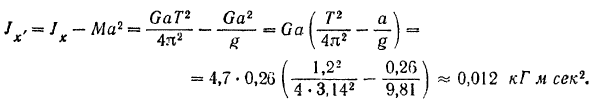
Эта теория взята с полного курса лекций на странице решения задач с подробными примерами по предмету теоретическая механика:
Теоретическая механика — задачи с решением и примерами
Возможно вам будут полезны эти дополнительные темы:

