Оглавление:









Фазовые портреты линейных систем
- На этом этапе рассмотрим фазовую траекторию и фазовый портрет линейной системы. При решении задач построения фазового портрета в линейных системах необходимо соблюдать следующую последовательность действий. Выберите систему координат так, чтобы ее начальная точка совпадала с положением равновесия системы. Создайте дифференциальное уравнение движения.
Исключить из уравнения время и интегрировать дифференциальные уравнения полученных фазовых траекторий для нахождения зависимости между отклонением системы обобщенными координатами и ее обобщенной скоростью. 4 построить интегральную кривую на фазовой плоскости при различных начальных условиях движения и найти фазовый портрет системы. 5 фазовый портрет определяет характер движения и равновесия системы. Задача 20.16.Создайте фазовый портрет гармонического генератора без затухания. Solution.
Определить закон вынужденных крутильных колебаний твердого тела, если его момент инерции относительно оси г, направленной вдоль проволоки, равен Л,. Людмила Фирмаль
Гармонические не ослабляющие осцилляторы, действие восстанавливающей силы, пропорциональное отклонению системы от ее равновесного положения, вызывают колебания, называемые свободой, и всегда стремятся вернуть систему в равновесное положение. Примеры гармонических неуплотняющих генераторов включают подпружиненную нагрузку, математический и физический маятник с малым углом отклонения который не учитывает сопротивление и электрический генератор, который состоит из емкости и индуктивности, но не имеет сопротивления.
Во всех этих случаях вид дифференциальных уравнений движения имеет вид X A x 0, 1 Где x-отклонение системы от положения равновесия или заряд электрического колебательного контура см. Главу 8, A s t-нагрузка, приложенная к пружине c-коэффициент жесткости, t-масса, длина маятника, сила тяжести, k Pa физическое ускорение где Pa —вес маятника, a —вес подвески, а —момент, л2 1 CB-для электрического колебательного контура I-индуктивность, C-емкость. Похлопывание Уравнение 1 в виде системы Если вы исключите время из этой системы, вы найдете yu k x yh y.
Единственной специальной точкой этого дифференциального уравнения является положение равновесия, когда правая часть 2 становится неопределенной, начало координат x 0 и y 0.При разделении переменной у Ю-На х ых. 3 Когда вы интегрируете 4 Где C — любая постоянная интегрирования, определяемая начальными условиями движения. Уравнение 4 представляет собой фазовый портрет системы. Это семейство эллипсов см. рис.20.3 симметрично относительно сингулярности симметрии.
Каждый эллипс-это фазовая орбита. Сингулярность центр определяется из 4 как эллипс, вырождающийся в точку при начальных условиях, соответствующих C 0. Какие эллипсы соответствуют периодическому движению системы Его параметры зависят только от начальных условий движения. Если задано начальное условие, то точка изображения представляет собой тот же эллипс, что и при перемещении по всему изображению. system. So, каждая из интегральных кривых в этом случае является всей фазовой траекторией.
Период колебаний не зависит от начальных условий движения. Поэтому любые эллипсы, представляющие точки, записываются со скоростью YЛ В то же время, идите по часовой стрелке. Отметим, что уравнение 4, в то же время, является законом сохранения механической энергии движения и потенциала рассматриваемой консервативной системы. Задача 20.17.Найти фазовый портрет гармонического датчика вязкого трения. Solution. In гармонические осцилляторы с вязким трением, сопротивление вязкое трение, электрическое сопротивление добавляется к восстанавливающей силе. Это пропорционально скорости и первой скорости в противоположном направлении.
Учитывая сопротивление, дифференциальное уравнение движения системы выглядит следующим образом X 2lL4-A x 0, 1 Где 2n a a, a — коэффициент пропорциональности сопротивления YaL — aL. Величина n имеет то же измерение, что и k, т. е. с-1, Если время измеряется в seconds. As перед тем, как представить I y, перепишем уравнение 1 в виде системы из 2 уравнений 2 Ах 3 Если исключить время из этой системы — 2pu-к X г 4 Итак, сингулярность координатного уравнения — это положение равновесия, а неопределенность справа равна 0 0. 4 является началом нарисованного part. To разделите переменные в выражении 4, внесите изменения.
Уравнение 4 принимает вид г-ых гг х-ый 2стр к. Интегрирование этого уравнения зависит от типа корня многочлена, возведенного в квадрат знаменателя с правой стороны. Поэтому рассмотрим отдельно 2 случая n k — для низкого сопротивления и n k-для высокого resistance. It также примыкает к граничному случаю n-K. Для низкого уровня resistance. In в этом случае при n k форма Интеграла 5 имеет вид Х4-2ld а 2 с ехр — — а С18, б Где AA2 — I2, C-произвольная интегральная константа.
Возвращаясь к старой переменной, т. е. r y заменяя x, находим уравнение интегральной кривой У2 2ll a2l по-2-с ехр АГС е х 7 Полученное уравнение интегральной кривой становится более заметным при переходе к новой переменной. Новая переменная становится новой декартовой координатой. После преобразования У2 2 л. ху k2×2 г ЛК 2 kgx2 Х2 y2 7 вместо С1 ехр 2 — — АГС г — -. 8 Введем полярные P и p. Х1 pCO8f, У1 p51n п. Уравнение 8 принимает вид Р схема ГФ. 9 Направление движения точки визуализации рис.
- А соответствует движению по часовой стрелке. Угол Р отсчитывается в противоположном направлении. Таким образом, в уравнении 9, угол Р непрерывно уменьшается. Это означает, что радиус-вектор точки изображения p также уменьшается бесконечно. Интегральная кривая-закручивающаяся спираль рисунок а, наматывающаяся к началу координат. Каждая интегральная кривая в этом случае является фазовой траекторией. Абсолютное значение фазовой скорости остается неизменным. o V x2 2 V y2 2 Lu k2×2.
Поскольку фазовая скорость бесконечно уменьшается по мере приближения точки визуализации к ее равновесному положению, точка визуализации не может достичь начала координат за ее пределами. Выпуск 20.1-7 к. Время, но приближается асимптотически. Сингулярность в этом случае называется стационарным фокусом. В начальных условиях точки изображения стремятся к началу координат, поэтому равновесие системы, соответствующей началу координат, стабилизируется.
Так как требуется определить только вынужденные крутильные колебания шара, то решение задачи сводится к отысканию частного решения уравнения (1). Людмила Фирмаль
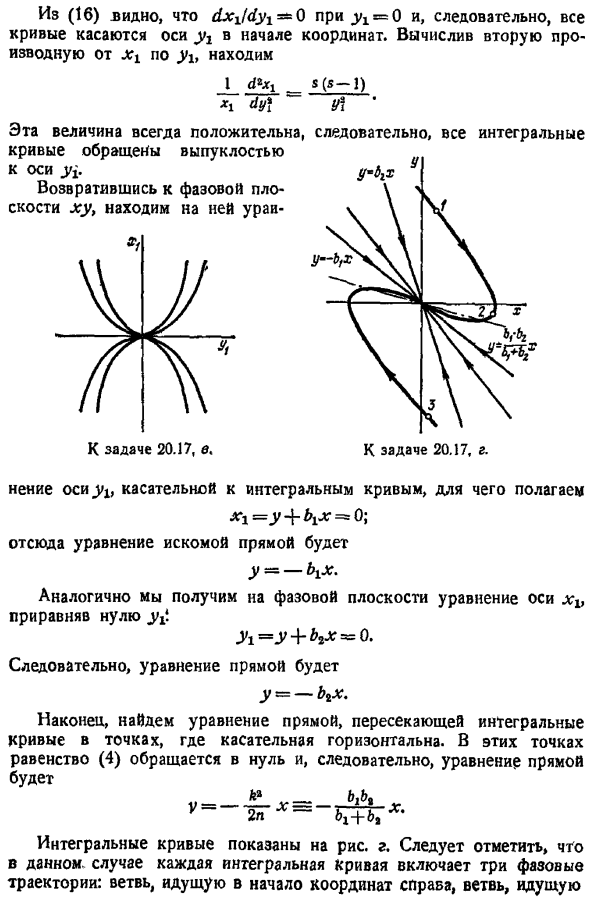
Линейное преобразование x1 A1x, A 5 xx не изменяет характер интегрирования curve. In дело в том, что если значения p k1 на плоскости спирали малы, то они близки к окружности Этот круг превращается в эллипс с небольшим значением n C при возврате к исходной переменной У2- — 2phu — — k2×2 со Таким образом, в плоскости xy спираль фазового локуса ближе к этому эллипсу рисунок B. Определите шаг спирали рисунок а. Из диаграммы видно, что шаг спирали равен xn-xn 1.С другой стороны, как известно, решение исходного дифференциального уравнения 1 имеет вид х ае-Р п А8- — — 11 Здесь воздух определяется начальными условиями движения.
Период колебаний равен t 2l Шаг спирали будет равен хп-ху 1 А-А- М А 1-е- для nT 1 уравнение 13 может быть приблизительно представлено расширением набора функций. 1-й- 1- 1-л — — … 12 13 Тогда шаг представляется приближенной формулой хп — хп 1 Апт. Поэтому в nT 1 шаг спирали пропорционален логарифмическому уменьшению. Если сопротивление большое. если мы интегрируем уравнение 5 для n k и введем полученный результат читать и находить г За — — 2яу4-АХА 14 Правая часть этого уравнения легко учитывается следующим образом y2 2n xy kgx y nxy- n-A8×2 — y b2x y b x , введите обозначение, чтобы сделать его кратким Б н-уя — К2,б н уя — к.
Уравнение 14 можно записать в виде Су с Су М 6 15 учитывая, что uy равно и равно ХХ г ВХ, ух г ВХ В качестве новой декартовой координаты уравнение 15, определяющее семейство интегральных кривых, принимает вид 16 где S г 6×1.Интегральная кривая показана на рисунке. С. 16 от LX СГР — O для x 0, поэтому все кривые находятся в контакте с осью Y1 в начале координат. если посчитать, то 2-я производная от Х в отношении г, Я Нет. 1 5 5-1 u и Это значение всегда положительное, и кривая выпуклая относительно оси y. Когда вы вернетесь на фазовую плоскость xy Выпуск 20.17, С. Поэтому все интегралы Выпуск 20.17, Г. 1 Y M изменение касательной оси yb к интегральной кривой, задающей M 0.
Отсюда уравнение искомой линии выглядит так — M- Аналогично получаем уравнения оси Х на фазовой плоскости. L 3 M 0- Таким образом, уравнение линии является у — ВХ. Наконец, найдите уравнение для линии, которая пересекает кривую интегрирования в точке, где касательная равна horizontal. At в этих точках уравнение 4 исчезает, и поэтому уравнение прямой выглядит так Год — б б 2Н 6, х Интегральная кривая показана на рисунке. d. обратите внимание, что в этом случае каждая кривая интегрирования содержит 3 фазовых локуса ветви к правому началу координат, ветви к левому началу координат и singularity.
В этом случае по всем фазовым траекториям точка изображения перемещается к началу координат и от сингулярного узла к стабильному узлу. Характер апериодического движения, осуществляемого исходной механической системой, легко определяется расположением точек изображения на фазовой траектории. Если точка визуализации в первый момент находится в положении, то ее скорость изначально положительна, и расстояние от положения равновесия системы визуализации увеличивается до тех пор, пока точка визуализации не пересечет ось dg. Тогда скорость будет отрицательной, и начальная система окажется асимптотически близкой к положению равновесия.
Если в первый момент точка изображения находится в положении 2, исходная система будет двигаться асимптотически Восемь х ст г- tG СТ Р Т с с Положение равновесия, поскольку отклонение системы является положительным, а скорость направлена в отрицательное направление оси X. Задача 20.18.Тело, лежащее на горизонтальной, негладкой поверхности, прикреплено к стене пружиной рисунок а. Коэффициент жесткости пружины c, максимальное значение сушильной кулоновской силы трения R. сила трения при движении постоянна по абсолютной величине и направлена в противоположную сторону от скорости. Начало отсчета выбирается в конце пружины, которая не растягивается.
Тело в первый момент освободилось, переместившись на расстояние x0 Тири без начальной скорости. Найти уравнение движения тела, а в случае 0 12—построить зависящие от времени и фазы траектории перемещений. Решение. Создайте дифференциальное уравнение движения Тело ТЯ-Щ Р 1 Знак минус соответствует положительной проекции скорости и знак плюс соответствует отрицательной проекции скорости на оси X. Показано в П К П Д SOP81 И Максимальное отклонение тела, в котором сила трения уравновешивается реакцией пружины от положения, в котором пружина не растягивается. в этом случае выражение 1 можно записать в виде пг с с х Д О 2 Или х А х Д 0 Вот, Си м к. Поставил г.
А потом… — , А х Д Отсюда Ла х-Д 1х г Или после интеграции — — х Г С. 3 Для этого интеграла знак плюс соответствует Y-y 0 и минус-Y y 0. Предположим, что первый момент 0 имеет x x0 0,а Y y 0.Сразу после начала упражнения y-x 0, а в Формуле 3 Нужно взять знак минус. Найти уравнение окружности вокруг точки. V координата x D, y 0.in в случае x-x1 объект теряет скорость и движется вверх x y 0. в Формуле 3 необходимо использовать знак плюс. Получим уравнение окружности вокруг точки A1 — D, 0.Точка xy симметрична относительно L, x0, а точка xy симметрична относительно M, xg и так далее.
Смотрите также:
Предмет теоретическая механика
| Вынужденные нелинейные колебания | Дельта-метод |
| Исследование нелинейных колебаний на фазовой плоскости. Основные определения | Автоколебания. Примеры автоколебательных систем |

